如图所示，在直角坐标系xOy第二、三象限存在有界匀强磁场Ⅰ（垂直纸面向里）和有界匀强磁场Ⅱ（垂直纸面向外），O、M、N、Q为磁场边界和x轴交点，OM=MN=L，在第二、三象限加上竖直向下的匀强电场。一质量为m，电荷量为q的带负电的小球从第一象限的P点（2L，L）以某一初速度沿-x轴方向射出，恰好从坐标原点O进入有界磁场Ⅰ，又从M点射出有界磁场Ⅰ，在有界磁场中做匀速圆周运动。（已知重力加速度为g）
（1）求所加匀强电场场强E的大小；
（2）求带电小球过原点O的速度大小和有界磁场Ⅰ的磁感应强度B的大小；
（3）如带电小球能再次回到原点O，则有界磁场Ⅱ的宽度应该满足的条件。
一列简谐横波沿x轴传播，某时刻t=0的图象如图所示，经过
的时间，这列波恰好第三次重复出现图示的波形。
（i）该列波的传播速度；
（ii）画出
时刻的波形。
两列简谐横波分别沿x轴正方向和负方向传播，两波源分别位于x=-0.2m和x=1.2m处，两列波的波速均为v=0.4m/s，波源的振幅均为A=2cm，图示为t=0时刻两列波的图象，此刻平衡位置在x=0..2m和x=0.8m的P、Q两质点恰好开始振动。质点M的平衡位置位于x=0.5m处。求：
①两波相遇的时刻；
②至t=1.5s时刻质点M运动的路程。
一列横波在x轴上传播，在tl=0时刻波形如图中实线所示，t2=0.05s时刻波形如图中虚线所示,且此时x=6m处的质点正从平衡位置向下振动.
①这列波的振幅和波长；
②已知
，波速大小及方向.
半径为R的
透明圆柱体固定于地面上，透明体对红光的折射率为n=2，如图所示。今让一束平行于地面的红光射向圆柱体左侧，经折射红光照射到右侧地面上。求圆柱体右侧地面上的黑暗部分长度。
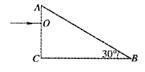
如图所示，直角三棱镜折射率为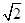
，∠B=30°，一束单色光垂直于AC面射向棱镜，人射点为O，求出光射出棱镜时的折射角。(不考虑BC面对光线的反射）