已知一次函数的图象经过点(0,4),并且与直线y=﹣2x相交于点(2,m),求这个一次函数的解析式.
从2开始,将连续的偶数相加,和的情况有如下规律:
2=1×2,
2+4=6=2×3,
2+4+6=12=3×4,
2+4+6+8=20=4×5,
2+4+6+8+10=30=5×6,
2+4+6+8+10+12=42=6×7,
……
按此规律,从2开始连续2011个偶数相加,其和是多少?
从2开始连续n个偶数相加,和是多少
1000+1002+1004+1006+……+2012的和是多少?
学校组织同学到博物馆参观,小明因事没有和同学同时出发,于是准备在学校门口搭乘出租车赶去与同学们会合,出租车的收费标准是:起步价为6元,3千米后每千米收1.2元,不足1千米的按1千米计算.请你回答下列问题小明乘车3.8千米,应付费_________元
小明乘车X(X是大于3的整数)千米,应付费多少钱?
小明身上仅有10元钱,乘出租车到距学校7千米远的博物馆的车费够不够?请说明理由.
如果规定符号“﹡”的意义是 ﹡
﹡ =
= ,求2﹡
,求2﹡ ﹡4的值.
﹡4的值.
已知a是最大的负整数,b是—2的相反数,c与d互为倒数,计算:a+b—cd的值.
先化简,再求值.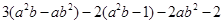 ,其中,
,其中,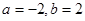 .
.