如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F.
(1)求证:AEPF是矩形;
(2)D为BC中点,连接DE,DF.求证:DE=DF.
某书店老板去批发市场购买某种图书,第一次购用100元,按该书定价2.8元现售,并快售完.由于该书畅销,第二次购书时,每本的批发价已比第一次高0.5元,用去了150元,所购数量比第一次多10本.当这批书售出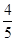 时,出现滞销,便以定价的5折售完剩余的图书,试问该老板第二次售书是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
时,出现滞销,便以定价的5折售完剩余的图书,试问该老板第二次售书是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
如图,在△ABC中,∠C=90°,AC+BC=9,点O是斜边AB上一点,以O为圆心2为半径的圆分别与AC、BC相切于点D、E。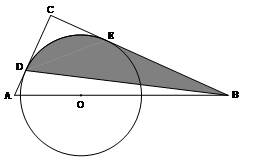
(1)求AC、BC的长;
(2)若AC=3,连接BD,求图中阴影部分的面积(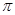 取3.14)。
取3.14)。
如图,一次函数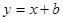 的图象经过点B(
的图象经过点B(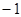 ,0),且与反比例函数
,0),且与反比例函数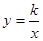 (
( 为不等于0的常数)的图象在第一象限交于点
为不等于0的常数)的图象在第一象限交于点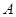 (1,
(1,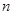 ).求:
).求: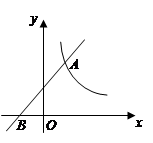
(1)一次函数和反比例函数的解析式;
(2)当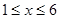 时,反比例函数
时,反比例函数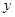 的取值范围.
的取值范围.
某书店把一本新书按标价的九折出售,仍可获利20%,若该书的进价为21元,则标价为
| A.26元 | B.27元 | C.28元 | D.29元 |
如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A,B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止.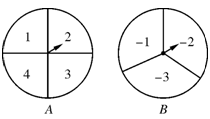
(1)用画树状图或列表法求乙获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由.