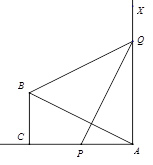
【改编】如图,有一个直角三角形ABC,∠ACB=90°,AC=10,BC=5,一条线段PQ=AB,P.Q两点分别在射线AC和过点A且垂直于AC的射线AX上运动,连接BQ,当ΔABC与ΔPQA全等时.BQ的长为( )
某摩托车厂本周内计划每日生产300辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减 |
-5 |
+7 |
-3 |
+4 |
+10 |
-9 |
-25 |
(1)本周三生产了多少辆摩托车?
(2)本周总生产量与计划生产量相比,是增加还是减少?
(3)产量最多的一天比产量最少的一天多生产了多少辆?
检修组乘汽车,沿公路检修线路,约定向东为正,向西为负,某天自A地出发, 到收工时,行走记录为(单位:千米):
+8、-9、+4、+7、-2、-10、+18、-3、+7、+5
回答下列问题:(每题5分,共10分)
(1)收工时在A地的哪边?距A地多少千米?
(2)若每千米耗油0.3升,问从A地出发到收工时,共耗油多少升?
若│a│=2,b=-3,c是最大的负整数,求a+b-c的值.
某商场老板对今年上半年每月的利润作了如下记录:1、2、5、6月盈利分别是13万元、12万元、12.5万元、10万元,3、4月亏损分别是0.7万元和0.8万元。试用正、负数表示各月的利润,并算出该商场上半年的总利润额。
小明做了四个正方形或长方形纸板如图1所示a、b为各边的长,小明用这四个纸板拼成图2图形,验证了完全平方公式。小明说他还能用这四个纸板通过拼接、遮盖,组成新的图形,来验证平方差公式.他说的是否有道理?如有道理,请你帮他画出拼成的图形.如没有道理、不能验证,请说明理由.并与同伴交流.

图1 (a+b)2=a2+2ab+b2
图2