如下图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第9个图形需要黑色棋子的个数是
| A.99 | B.80 | C.63 | D.132 |
某商店在某一时间以每件50元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,在这次买卖中,该家商店()
| A.亏损6.7元 |
| B.盈利6.7元 |
| C.不亏不盈 |
| D.以上都不正确 |
已知抛物线y=ax2+bx+c,a>0,c>1.当x=c时,y=0;当0<x<c时,y>0,则()
| A.ac≥1 | B.ac≤1 | C.ac>1 | D.ac<1 |
已知抛物线y=ax2+bx+c与x轴的两个公共点之间的距离为1.若将抛物线y=ax2+bx+c向上平移一个单位,则它与x轴只有一个公共点;若将抛物线y=ax2+bx+c向下平移一个单位,则它经过原点,则抛物线y=ax2+bx+c为()
A.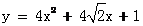 |
B.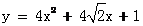 或 或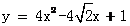 |
C.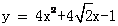 |
D.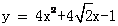 或 或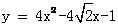 |
在比例尺为1:10000000的地图上,量的甲、乙两地的距离是30cm,则两地的实际距离是()
| A.30km | B.300km | C.3000km | D.30000km |
如图,PQ、PR、AB是⊙O的切线,切点分别为Q、R、S,若∠APB=40°,则∠A0B等于()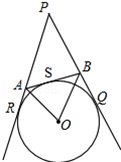
| A.40° | B.50° | C.60° | D.70° |