设ω>0,函数y=sin(ωx+ )+2的图象向右平移
)+2的图象向右平移 个单位后与原图象重合,则ω的最小值是( )
个单位后与原图象重合,则ω的最小值是( )
A. |
B. |
C. |
D.3 |
使奇函数f(x)=sin(2x+α)在[- ,0]上为减函数的α值为( )
,0]上为减函数的α值为( )
A. |
B.π | C.- |
D.2π |
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)满足条件f(x+ )+f(x)=0,则ω的值为( )
)+f(x)=0,则ω的值为( )
| A.2π | B.π | C. |
D. |
已知函数f(x)=sin(2x- ),若存在a∈(0,π),使得f(x+a)=f(x-a)恒成立,则a的值是( )
),若存在a∈(0,π),使得f(x+a)=f(x-a)恒成立,则a的值是( )
A. |
B. |
C. |
D. |
函数y=- cos2x+
cos2x+ 的递增区间是( )
的递增区间是( )
A.(kπ,kπ+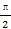 )(k∈Z) )(k∈Z) |
B.(kπ+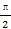 ,kπ+π)(k∈Z) ,kπ+π)(k∈Z) |
| C.(2kπ,2kπ+π)(k∈Z) |
| D.(2kπ+π,2kπ+2π)(k∈Z) |