已知某隧道截面积拱形为抛物线形，拱顶离地面10米，底部款20米．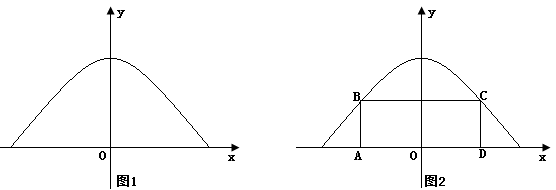
（1）建立如图1所示的平面直角坐标系，使y轴为抛物线的对称轴，x轴在地面上．求这条抛物线的解析式；
（2）维修队对隧道进行维修时，为了安全，需要在隧道口搭建一个如图2所示的矩形支架AB-BC-CD（其中B、C两点在抛物线上，A、D两点在地面上），现有总长为30米的材料，那么材料是否够用？
（3）在（2）的基础上，若要求矩形支架的高度AB不低于5米，已知隧道是双向行车道，正中间用护栏隔开，则同一方向行驶的两辆宽度分别为4米，高度不超过5米的车能否并排通过隧道口？（护栏宽度和两车间距忽略不计）
（本小题8分）
关于x的一元二次方程
有两个不相等的实数根．
（1）求k的取值范围．
（2）请选择一个k的负整数值，并求出方程的根
计算或化简：（本小题6分）
解下列方程（每题5分，共10分）
（1）
（2）
（用配方法解）
如图①②，在平面直角坐标系中，边长为2的等边△CDE恰好与坐标系中的△OAB重合，现将△CDE绕边AB的中点G(G点也是DE的中点)，按顺时针方向旋转180°到△C1DE的位置．
(1)求C1点的坐标；
(2)求经过三点O、A、C1的抛物线的解析式；
(3)如图③，⊙G是以AB为直径的圆，过B点作⊙G的切线与x轴相交于点F，求切线BF
的解析式；
(4)抛物线上是否存在一点M，使得
．若存在，请求出点M的坐标；
若不存在，请说明理由．
(1)计算:如图①,直径为
的三等圆⊙O
、⊙O
、⊙O
两两外切，切点分别为A、B、C ，求OA的长（用含的代数式表示）.
（2）探索:若干个直径为的圆圈分别按如图10②所示的方案一和如图10③所示的方案二的方式排放，探索并求出这两种方案中
层圆圈的高度
和
（用含、的代数式表示）.
（3）应用:现有长方体集装箱，其内空长为5米，宽为3.1米，高为3.1米.用这样的集装箱装运长为5米，底面直径（横截面的外圆直径）为0.1米的圆柱形钢管，你认为采用（2）中的哪种方案在该集装箱中装运钢管数最多？并求出一个这样的集装箱最多能装运多少根钢管？（
≈1.73）