若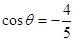
，
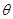是第三象限的角,则
=（ ）
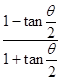A． |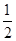
B． |
C． |
D．-2 |
反证法证明三角形的内角中至少有一个不小于60°，反设正确的是（）
| A．假设三内角都不大于60° | B．假设三内角都小于60° |
| C．假设三内角至多有一个大于60° | D．假设三内角至多有两个小于60° |
用反证法证明：“方程ax2+bx+c=0，且a，b，c都是奇数，则方程没有整数根”正确的假设是方程存在实数根x0为（）
| A．整数 | B．奇数或偶数 | C．正整数或负整数 | D．自然数或负整数 |
用反证法证明命题：“若整数系数一元二次方程ax2+bx+c=0（a≠o）有有理根，那么 a，b，c中至少有一个是偶数”时，应假设（）
| A．a，b，c中至多一个是偶数 |
| B．a，b，c中至少一个是奇数 |
| C．a，b，c中全是奇数 |
| D．a，b，c中恰有一个偶数 |
“用反证法证明命题“如果x＜y，那么x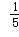
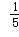＜y”时，假设的内容应该是（）
A．x =y |
| B．x＜y |
| C．x=y且x＜y |
D．x =y或x＞y |
用反证法证明：将9个球分别染成红色或白色，那么无论怎么染，至少有5个球是同色的．其假设应是（）
| A．至少有5个球是同色的 | B．至少有5个球不是同色的 |
| C．至多有4个球是同色的 | D．至少有4个球不是同色的 |