设函数f(x)在R上可导，其导函数为f′(x)，且函数y＝(1－x)f′(x)的图象如图所示，则下列结论中一定成立的是( )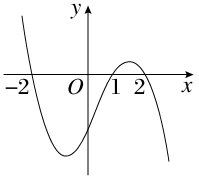
| A．函数f(x)有极大值f(2)和极小值f(1) |
| B．函数f(x)有极大值f(－2)和极小值f(1) |
| C．函数f(x)有极大值f(2)和极小值f(－2) |
| D．函数f(x)有极大值f(－2)和极小值f(2) |
若a>0，b>0，且函数f(x)＝4x3－ax2－2bx－2在x＝1处有极值，则ab的最大值为( )
| A．2 | B．3 | C．6 | D．9 |
函数f(x)＝x2－2lnx的单调递减区间是( )
| A．(0,1] | B．[1，＋∞) |
| C．(－∞，－1]∪(0,1] | D．[－1,0)∪(0,1] |
经过原点且与曲线y＝
相切的方程是( )
A．x＋y＝0或 ＋y＝0 |
B．x－y＝0或＋y＝0 |
| C．x＋y＝0或－y＝0 |
D．x－y＝0或－y＝0 |
定义在R上的函数f(x)的导函数为f′(x)，已知f(x＋1)是偶函数，(x－1)f′(x)<0．若x1<x2，且x1＋x2>2，则f(x1)与f(x2)的大小关系是( )
| A．f(x1)<f(x2) | B．f(x1)＝f(x2) |
| C．f(x1)>f(x2) | D．不确定 |
上单调递减的函数为（ ）
