(本小题满分14分)如图,已知三棱锥A—BPC中,AP⊥PC, AC⊥BC,M为AB中点,D为PB中点, 且△PMB为正三角形.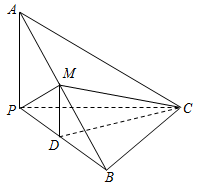
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D—BCM的体积.
已知与圆C:x2+y2-2x-2y+1=0相切的直线l交x轴,y轴于A,B两点,
OA|=a,|OB|=b(a>2,b>2).
(Ⅰ)求证:(a-2)(b-2)=2;
(Ⅱ)求线段AB中点的轨迹方程;
(Ⅲ)求△AOB面积的最小值.
在平面直角坐标系 中,点P到两点
中,点P到两点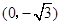 ,
, 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为 .
.
(Ⅰ)写出C的方程;
(Ⅱ)设直线 与C交于A,B两点.k为何值时
与C交于A,B两点.k为何值时

 ?此时
?此时 的值是多少?
的值是多少?
在 中,内角
中,内角 对边的边长分别是
对边的边长分别是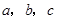 ,已知
,已知 ,
,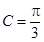 .
.
(Ⅰ)若 的面积等于
的面积等于 ,求
,求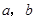 ;
;
(Ⅱ)若 ,求
,求 的面积.
的面积.
等差数列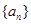 的各项均为正数,
的各项均为正数, ,前
,前 项和为
项和为 ,
,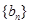 为等比数列,
为等比数列,  ,
,
且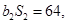
 .
.
(Ⅰ)求 与
与 ;
;
(Ⅱ)求和: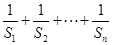 .
.
袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分为1,2.
(Ⅰ)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(Ⅱ)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.