某校进行校园卫生大扫除，七年级一班原计划分成两个小组，第一组26人打扫大操场，第二组22人打扫班级的包干卫生区．后来根据工作实际需要，要使第二组人数是第一组人数的2倍，那么应从第一组调多少人到第二组？
（1）设应从第一组调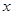
人到第二组，依题意填表（用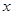的代数式表示）：
| 组 别 |
第一组 |
第二组 |
| 原计划小组的人数（单位：人） |
26 |
22 |
| 调整后小组的人数（单位：人） |
|
|
（2）根据以上表格列出方程，求出应从第一组调多少人到第二组？
（钦州）如图，船A、B在东西方向的海岸线MN上，均收到已触礁搁浅的船P的求救信号，已知船P在船A的北偏东60°方向上，在船B的北偏西37°方向上，AP=30海里．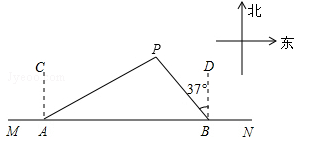
（1）尺规作图：过点P作AB所在直线的垂线，垂足为E（要求：保留作图痕迹，不写作法）；
（2）求船P到海岸线MN的距离（即PE的长）；
（3）若船A、船B分别以20海里/时、15海里/时的速度同时出发，匀速直线前往救援，试通过计算判断哪艘船先到达船P处．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
（钦州）如图，在矩形ABCD中，点E、F分别是边AB、CD的中点．求证：DE=BF．
（柳州）如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=12cm，BC=18cm，点P从点A出发以2cm/s的速度沿A→D→C运动，点P从点A出发的同时点Q从点C出发，以1cm/s的速度向点B运动，当点P到达点C时，点Q也停止运动．设点P，Q运动的时间为t秒．
（1）从运动开始，当t取何值时，PQ∥CD？
（2）从运动开始，当t取何值时，△PQC为直角三角形？
（柳州）如图，在△ABC中，D为AC边的中点，且DB⊥BC，BC=4，CD=5．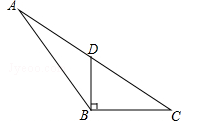
（1）求DB的长；
（2）在△ABC中，求BC边上高的长．
（来宾）在矩形ABCD中，AB=a，AD=b，点M为BC边上一动点（点M与点B、C不重合），连接AM，过点M作MN⊥AM，垂足为M，MN交CD或CD的延长线于点N．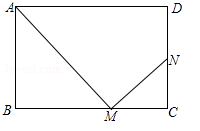
（1）求证：△CMN∽△BAM；
（2）设BM=x，CN=y，求y关于x的函数解析式．当x取何值时，y有最大值，并求出y的最大值；
（3）当点M在BC上运动时，求使得下列两个条件都成立的b的取值范围：①点N始终在线段CD上，②点M在某一位置时，点N恰好与点D重合．