(本小题满分14分)已知椭圆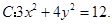
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)设椭圆 上在第二象限的点
上在第二象限的点 的横坐标为
的横坐标为 ,过点
,过点 的直线
的直线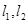 与椭圆
与椭圆 的另一交点分别为
的另一交点分别为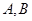 .且
.且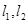 的斜率互为相反数,
的斜率互为相反数,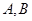 两点关于坐标原点
两点关于坐标原点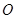 的对称点分别为
的对称点分别为 ,求四边形
,求四边形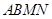 的面积的最大值.
的面积的最大值.
(本小题满分13分)如图,已知抛物线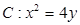 ,过焦点F任作一条直线与
,过焦点F任作一条直线与 相交于
相交于 两点,过点
两点,过点 作
作 轴的平行线与直线
轴的平行线与直线 相交于点
相交于点 (
( 为坐标原点).
为坐标原点).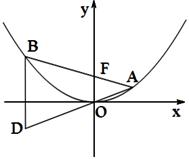
(Ⅰ)证明:动点 在定直线上;
在定直线上;
(Ⅱ)点P为抛物线C上的动点,直线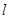 为抛物线C在P点处的切线,求点Q(0,4)到直线
为抛物线C在P点处的切线,求点Q(0,4)到直线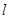 距离的最小值.
距离的最小值.
(本小题满分13分)在四棱锥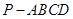 中,
中,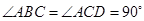 ,
,
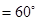 ,
,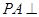 平面
平面 ,直线PC与平面ABCD所成角为
,直线PC与平面ABCD所成角为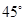 ,
,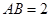 .
.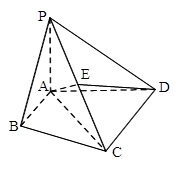
(Ⅰ)求四棱锥 的体积
的体积 ;
;
(Ⅱ)若 为
为 的中点,求证:平面
的中点,求证:平面
 平面
平面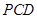 .
.
(本小题满分13分)设 是公比为q的等比数列.
是公比为q的等比数列.
(Ⅰ)推导 的前n项和公式;
的前n项和公式;
(Ⅱ)设q≠1, 证明数列 不是等比数列.
不是等比数列.
(本小题满分12分)已知向量 ,向量
,向量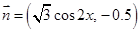 ,函数
,函数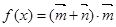 .
.
(Ⅰ)求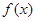 的最小正周期
的最小正周期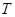 ;
;
(Ⅱ)已知 分别为
分别为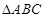 内角
内角 的对边,
的对边,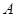 为锐角,
为锐角,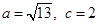 ,且
,且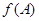 恰是
恰是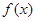 在
在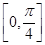 上的最大值,求
上的最大值,求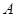 和
和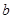 .
.
(本小题满分12分)已知二次函数 .
.
(1)若 ,且对任意实数
,且对任意实数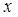 均有
均有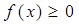 ,求
,求 的表达式;
的表达式;
(2)在(1)的条件下,当 时,设
时,设 ,求g(x)最小值.
,求g(x)最小值.