(本小题满分10分)如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA 平面ABCD,
平面ABCD,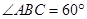 ,E,F分别是BC, PC的中点.
,E,F分别是BC, PC的中点.
(1)证明:AE⊥PD;
(2)若H为PD上的动点,EH与平面PAD所成最大角的正 切值为 ,求二面角E—AF—D的余弦值.
,求二面角E—AF—D的余弦值.
如图,在直三棱柱中 -A BC中,AB
-A BC中,AB  AC,AB=AC=2,
AC,AB=AC=2,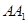 =4,点D是BC的中点.
=4,点D是BC的中点.
(1)求异面直线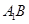 与
与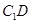 所成角的余弦值;
所成角的余弦值;
(2)求平面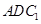 与
与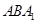 所成二面角的正弦值.
所成二面角的正弦值.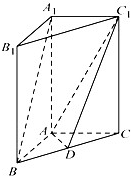
现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(1)求张同学至少取到1道乙类题的概率;
(2)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对每道甲类题的概率都是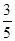 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是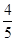 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用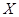 表示张同学答对题的个数,求
表示张同学答对题的个数,求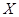 的分布列和数学期望.
的分布列和数学期望.
已知等差数列 的前
的前 项和为
项和为 ,
, ,
,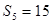 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)若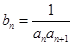 ,求数列
,求数列 的前100项和.
的前100项和.
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
由散点图可知,销售量 与价格
与价格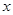 之间有较好的线性相关关系,其线性回归直线方程是;
之间有较好的线性相关关系,其线性回归直线方程是;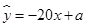
(1)求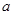 的值;
的值;
(2)预计在今后的销售中,销量与单价仍然服从线性回归直线方程中的关系,且该产品的成本是每件4元,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入一成本)
已知函数 ,且
,且 ,
, .
.
(1)求 、
、 的值;
的值;
(2)已知定点 ,设点
,设点 是函数
是函数 图象上的任意一点,求
图象上的任意一点,求 的最小值,并求此时点
的最小值,并求此时点 的坐标;
的坐标;
(3)当 时,不等式
时,不等式 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.