设实数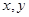 满足
满足 ,则
,则 的最大值是( )
的最大值是( )
A.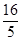 |
B.8 | C.9 | D.16 |
若集合A1,A2满足A1∪A2=A,则称(A1,A2)为集合A的一种分析,并规定:当且仅当A1=A2时,(A1,A2)与(A2,A1)为集合A的同一种分析,则集合A={a1,a2,a3}的不同分析种数是()
| A.4 | B.8 | C.27 | D.15 |
位于坐标原点的一个质点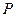 ,其移动规则是:质点每次移动一个单位,移动的方向向上或向右,并且向上、向右的概率都是
,其移动规则是:质点每次移动一个单位,移动的方向向上或向右,并且向上、向右的概率都是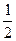 .质点
.质点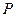 移动5次后位于(3,2)的概率是()
移动5次后位于(3,2)的概率是()
A.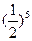 |
B. |
C.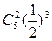 |
D.C |
一个质量均匀的正四面体型的骰子,其四个面上分别标有数字1、2、3、4,若连续抛掷三次,取这三次面向下的数字分别作为三角形的边长,则其能构成钝角三角形的概率为()
A.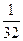 |
B.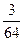 |
C.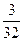 |
D. |
若 ,
,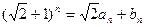
 ,则
,则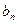 的值()
的值()
| A.一定是奇数 | B.一定是偶数 | C.与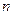 的奇偶性相反 的奇偶性相反 |
D.与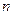 的奇偶性相同 的奇偶性相同 |
某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用,把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录做比较,提出假设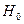 :“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算
:“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算 ,则下列说法正确的是()
,则下列说法正确的是()
| A.这种疫苗能起到预防甲型H1N1流感的有效率为1﹪ |
| B.若某人未使用该疫苗,则他在半年中有99﹪的可能得甲型H1N1 |
| C.有1﹪的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
| D.有99﹪的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |