(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E。
证明:DE=BD+CE。
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由。
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并给出证明。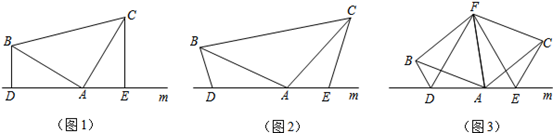
先将下列代数式化简,再求值:(a+b)(a﹣b)+b(b﹣2),其中a= ,b=1.
,b=1.
解下列不等式:2x﹣5≤2( ﹣3)
﹣3)
岳阳王家河流域综合治理工程已正式启动,其中某项工程,若由甲、乙两建筑队合做,6个月可以完成,若由甲、乙两队独做,甲队比乙队少用5个月的时间完成.
(1)甲、乙两队单独完成这项工程各需几个月的时间?
(2)已知甲队每月施工费用为15万元,比乙队多6万元,按要求该工程总费用不超过141万元,工程必须在一年内竣工(包括12个月).为了确保经费和工期,采取甲队做a个月,乙队做b个月(a、b均为整数)分工合作的方式施工,问有哪几种施工方案?
游泳池常需进行换水清洗,图中的折线表示的是游泳池换水清洗过程“排水﹣﹣清洗﹣﹣灌水”中水量y(m3)与时间t(min)之间的函数关系式.
(1)根据图中提供的信息,求整个换水清洗过程水量y(m3)与时间t(min)的函数解析式;
(2)问:排水、清洗、灌水各花多少时间?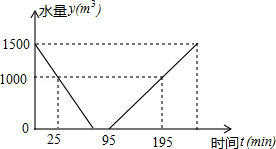
岳阳楼、君山岛去年评为国家5A级景区.“十•一”期间,游客满员,据统计绘制了两幅不完整的游客统计图(如图①、图②),请你根据图中提供的信息解答下列问题:
(1)把图①补充完整;
(2)在图②中画出君山岛“十•一”期间游客人次的折线图;
(3)由统计可知,岳阳楼、君山岛两景点“十一”期间共接待游客149000人次,占全市接待游客总数的40%,求全市共接待游客多少人次(用科学记数法表示,保留两位有效数字)
