(本题7分)为了决定谁将获得仅有的一张科普报告入场券,甲和乙设计了如下的一个游戏:口袋中有编号分别为1、2、3的红球三个和编号为4的白球一个,四个球除了颜色或编号不同外,没有任何别的区别,摸球之前将小球搅匀.先甲摸两次,每次摸出一个球;把甲摸出的两个球放回口袋后,乙再摸,乙只摸一个球.如果甲摸出的两个球都是红色,甲得1分,否则,甲得0分;如果乙摸出的球是白色,乙得1分,否则,乙得0分 ;得分高的获得入场券,如果得分相同,游戏重来.
(1)运用列表或画树状图求甲得1分的概率;
(2)这个游戏是否公平?请说明理由.
解不等式组 ,并用数轴表示其解集。
,并用数轴表示其解集。
如图,已知抛物线 (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(1)点B的坐标为,点C的坐标为(用含b的代数式表示);
(2)若b=8,请你在抛物线上找点P,使得△PAC是直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你探索,在(1)的结论下,在第一象限内是否存在点Q,使得△QCO、△QOA和△QAB中的任意两个三角形均相似(全等可看作相似的特殊情况)如果存在,求出点Q的坐标;如果不存在,请说明理由.
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系;
(1)根据图中信息,说明图中点(2,0)的实际意义;
(2)求图中线段AB所在直线的函数解析式和甲乙两地之间的距离;
(3)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;
如图,已知△ABC内接于⊙O,AC是⊙O的直径,D是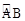 的中点,过点D作直线BC的垂线,分别交CB、CA的延长线E、F
的中点,过点D作直线BC的垂线,分别交CB、CA的延长线E、F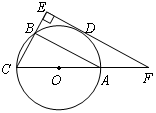
(1)求证:EF是⊙O的切线;
(2)若EF=12,EC=9,求⊙O的半径.
已知,如图:点A(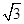 ,1)在反比例函数图象上,将y轴绕点O顺时针旋转30°,与反比例函数在第一象限内交于点B,
,1)在反比例函数图象上,将y轴绕点O顺时针旋转30°,与反比例函数在第一象限内交于点B,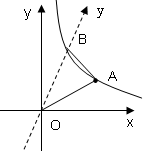
求:(1)反比例函数的解析式;
(2)求点B的坐标及△AOB的面积.