（本题12分）
九年级数学兴趣小组组织了以“等积变形”为主题的课题研究．
第一学习小组发现：如图（1），点A、点B在直线l1上，点C、点D在直线l2上，若l1∥l2，则S△ABC=S△ABD；反之亦成立．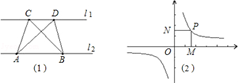
第二学习小组发现：如图（2），点P是反比例函数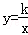
上任意一点，过点P作x轴、y轴的垂线，垂足为M、N，则矩形OMPN的面积为定值|k|．
请利用上述结论解决下列问题：
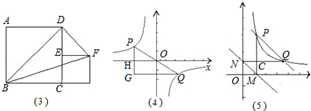
（1）如图（3），四边形ABCD、与四边形CEFG都是正方形点E在CD上，正方形ABCD边长为2，则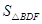
=_________．
（2）如图（4），点P、Q在反比例函数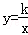图象上，PQ过点O，过P作y轴的平行线交x轴于点H，过Q作x轴的平行线交PH于点G，若
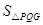=8，则
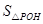=_________，k=_________．
（3）如图（5）点P、Q是第一象限的点，且在反比例函数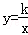图象上，过点P作x轴垂线，过点Q作y轴垂线，垂足分别是M、N，试判断直线PQ与直线MN的位置关系，并说明理由．
解不等式组：
，并把它的解集在数轴上表示出来．
已知正方形的面积是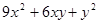
（x>0,y>0）,利用分解因式写出表示该正方形的边长的代数式.
根据题意填充理由：
已知：如下图所示，∠1=∠2.求证：∠3+∠4=180°.
证明：∵∠5=∠2（ ）.
又∠1=∠2（已知）.
∴∠5=∠1（ ）.
∴AB∥CD( ).
∴∠3+∠4=180°( ).
如图，在直角坐标系中，已知点A（-1，0）、B（0，2），将线段AB绕点A按逆时针方向旋转90°至AC．
（1）点C的坐标为（，）；
（2）若二次函数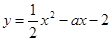
的图象经过点C．
①求二次函数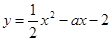的关系式；
②当-1≤x≤4时，直接写出函数值y对应的取值范围；
③在此二次函数的图象上是否存在点P（点C除外），使△ABP是以AB为直角边的等腰直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．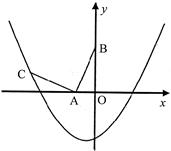 
数学实验室：小明取出一张矩形纸片ABCD，AD=BC=5，AB=CD=25．他先在矩形ABCD的边AB上取一点M，接着在CD上取一点N，然后将纸片沿MN折叠，使MB′与DN交于点K，得到△MNK（如图①）．
（1）试判断△MNK的形状，并说明理由．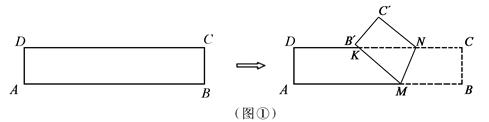
（2）如何折叠能够使△MNK的面积最大？请你利用备用图探究可能出现的情况，求出最大值．