操作：小英准备制作一个表面积为6cm2的正方体纸盒，现选用一些废弃的纸片进行如下设计：
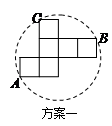
说明：
方案一：图形中的圆过点A.B.C；
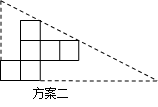
方案二：直角三角形的两直角边与展开图左下角的正方形边重合，斜边经过两个正方形的顶点．
纸片利用率=
×100%
发现：（1）小英发现方案一中的点A.B恰好为该圆一直径的两个端点．你认为小英的这个发现是否正确，请说明理由．
（2）小英通过计算，发现方案一中纸片的利用率仅约为38.2%．请帮忙计算方案二的利用率，并写出求解过程．（结果精确到0.1%）
探究：（3）小英感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直接写出方案三的利用率．（结果精确到0.1%）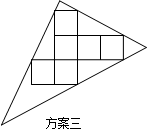
说明：方案三中的每条边均过其中两个正方形的顶点．
如图所示，在直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换成△OA2B2，第三次将△OA2B2变换成△OA3B3，已知A（1，3），A1（2，3），A2（4，3），A3（8，3），B（2，0），B1（4，0），B2（8，0），B3（16，0）．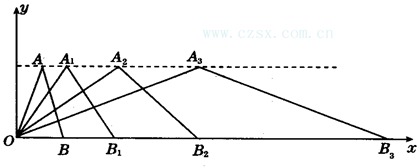
（1）观察每次变换前后的三角形有何变化，找出规律，按些变换规律将△OA3B3变换成△OA4B4，则A4的坐标是_______，B4的坐标是_________．
（2）若按第（1）题的规律将△OAB进行了n次变换，得到△OAnBn，比较每次变换中三角形顶点坐标有何变化，找出规律，请推测An的坐标是_______，Bn的坐标是_______．
在直角坐标系中，A（-3，4），B（-1，-2），O为原点，求三角形AOB的面积．
如图，一个机器人从O点出发，向正东方向走3米到达A1点，再向正北方向走6米到达A2点，再向正西方向走9米到达A3点，再向正南方向走12米到达A4点，再向正东方向走15米到达A5点，按如此规律走下去，当机器人走到A6点时，A6点的坐标是________．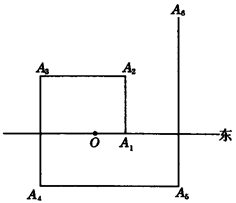
如图，三角形ABC是由三角形A1B1C1平移后得到的，三角形ABC中任意一点P（x，y）经平移后对应点为P1（x-3，y-5），求A1、B1、C1的坐标．
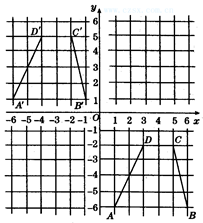
如图，梯形A′B′C′D′可以由梯形ABCD经过怎样的平移得到？对应点的坐标有什么变化？