如图,平行四边形ABCD中,CE⊥AB于E,若∠A=125°,则∠BCE的度数为( )
| A.35° | B.55° | C.25° | D.30° |
如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于( )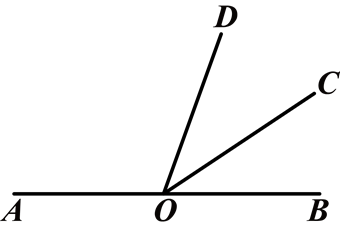
A.35°
B.70°
C.110°
D.145°
下列图形中,∠1与∠2是对顶角的是( )
A.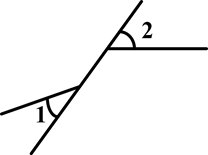 |
B.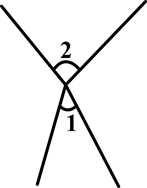 |
C.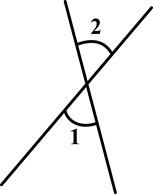 |
D.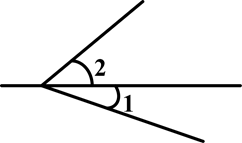 |
如图,直线AB、CD相交于O,OB是∠DOE的平分线,若∠COE=100°,则∠AOC=( )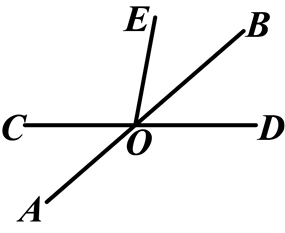
A.30°
B.40°
C.50°
D.60°
如图所示,∠1的邻补角是( )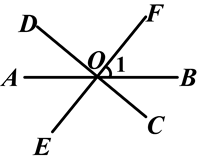
| A.∠BOC |
| B.∠BOE和∠AOF |
| C.∠AOF |
| D.∠BOC和∠AOF |
下列关于对顶角的语句中,正确的是( )
| A.对顶角不一定相等 |
| B.两条直线相交所成的角是对顶角 |
| C.有公共顶点并且相等的两个角是对顶角 |
| D.两条直线相交所成的四个角中,有公共顶点,无公共边的两个角是对顶角 |