(本小题满分12分)深圳市于2014年12月29日起实施小汽车限购政策.根据规定,每年发放10万个小汽车名额,其中电动小汽车占20%,通过摇号方式发放,其余名额通过摇号和竞价两种方式各发放一半.政策推出后,某网站针对不同年龄段的申请意向进行了调查,结果如下表所示:
| 申请意向 年龄 |
摇号 |
竞价(人数) |
合计 |
|
| 电动小汽车(人数) |
非电动小汽车(人数) |
|||
| 30岁以下 (含30岁) |
50 |
100 |
50 |
200 |
| 30至50岁 (含50岁) |
50 |
150 |
300 |
500 |
| 50岁以上 |
100 |
150 |
50 |
300 |
| 合计 |
200 |
400 |
400 |
1000 |
(1)采取分层抽样的方式从30至50岁的人中抽取10人,求其中各种意向人数;
(2)在(1)中选出的10个人中随机抽取4人,求其中恰有2人有竞价申请意向的概率;
(3)用样本估计总体,在全体市民中任意选取4人,其中摇号申请电动小汽车意向的人数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
一袋中有6个黑球,4个白球.
(1)依次取出3个球,不放回,已知第一次取出的是白球,求第三次取到黑球的概率;
(2)有放回地依次取出3球,已知第一次取的是白球,求第三次取到黑球的概率;
(3)有放回地依次取出3球,求取到白球个数X的分布列、期望和方差.
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 |
1至4件 |
5至8件 |
9至12件 |
13至16件 |
17件及以上 |
| 顾客数(人) |
 |
30 |
25 |
 |
10 |
| 结算时间(分钟/人) |
1 |
1.5 |
2 |
2.5 |
3 |
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(1)确定 的值,并求顾客一次购物的结算时间
的值,并求顾客一次购物的结算时间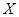 的分布列与数学期望;
的分布列与数学期望;
(2)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过 分钟的概率.(注:将频率视为概率)
分钟的概率.(注:将频率视为概率)
已知函数 ,且任意的
,且任意的

(1)求 、
、 、
、 的值;
的值;
(2)试猜想 的解析式,并用数学归纳法给出证明.
的解析式,并用数学归纳法给出证明.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个至多一个“成绩优秀”的概率;
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为:“成绩优秀”与教学方式有关.
| 甲班 (A方式) |
乙班 (B方式) |
总计 |
|
| 成绩优秀 |
|||
| 成绩不优秀 |
|||
| 总计 |
附: 
 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
| k |
1.323 |
2.072 |
2. 706 |
3. 841 |
5. 024 |
已知二项式 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求 的值;(2)设
的值;(2)设 .
.
①求 的值; ②求
的值; ②求 的值.
的值.