（14’）如图，在平面直角坐标系
中，A、B为
轴上两点，C、D为
轴上的两点，经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点C的坐标为（0，
），点M是抛物线C2：
（
＜0）的顶点．
（1）求A、B两点的坐标；
（2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；
（3）当△BDM为直角三角形时，求的值．
一游泳池长90米，甲、乙两人分别在游泳池相对两边同时朝另一边游泳，图中实线和虚线分别为甲、乙与游泳池一边的距离随游泳时间的变化而变化的图象，若不计转向时间，请回答下列问题：
（1）甲、乙游泳的平均速度各是多少？
（2）从开始到3分钟之间他们相遇了几次？
如图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图．根据图回答问题：
（1）9时，10时30分，12时所走的路程分别是多少？
（2）他休息了多长时间？
（3）他从休息后直至到达目的地这段时间的平均速度是多少？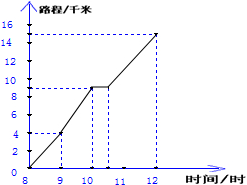
现行固定网通电话的通话收费标准为：前3分钟（不足3分钟按3分钟计）0.22元，3分钟后每分钟按0.11元（不足1分钟按1分钟计）．
（1）请填写下面的表格：
| 时间（分钟） |
1 |
2 |
3 |
4 |
5 |
6 |
… |
| 话费（元） |
（2）上述变化中，自变量和因变量分别是什么？
（3）通话10.5分钟时的话费是多少元？
某地区现有果树24000棵，计划今后每年栽果树3000棵．
（1）试用含年数x（年）的式子表示果树总棵数y（棵）；
（2）预计到第5年该地区有多少棵果树？
父亲告诉小明：“距离地面越远，温度越低，”并给小明出示了下面的表格．
| 距离地面高度（千米） |
0 |
1 |
2 |
3 |
4 |
5 |
| 温度（℃） |
20 |
14 |
8 |
2 |
﹣4 |
﹣10 |
根据上表，父亲还给小明出了下面几个问题，你和小明一起回答．
（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（2）如果用h表示距离地面的高度，用t表示温度，那么随着h的变化，t是怎么变化的？
（3）你能猜出距离地面6千米的高空温度是多少吗？
（4）你能写出h 与t 之间的关系式吗？