（本题10分）如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，反比例函数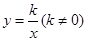
在第一象限内的图象经过点D，与AB相交于点E，且点B（4，2）．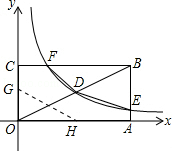
（1）求反比例函数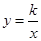
的关系式；
（2）求四边形OAED的面积；
（3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，若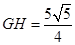
，求直线GH的函数关系式．
计算：①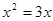
②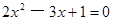
．
计算：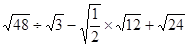
如图，在一块长为20m，宽为15m的矩形绿化带的四周扩建一条宽度相等的小路（图中阴影部分），建成后绿化带与小路的总面积为546m2，如果设小路的宽度为x m，那么下列方程正确的是（）
A． |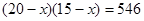
B． |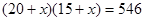
C． |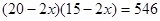
D． |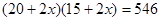
如图1，在△ABC中，AC=AB=2，∠A=90°，将一块与△ABC全等的三角板的直角顶点放在点C上，一直角边与BC重叠．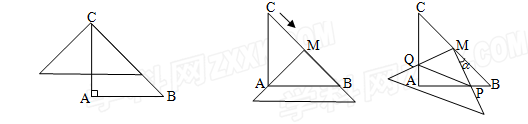
（1）操作1：固定△ABC，将三角板沿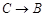
方向平移，使其直角顶点落在BC的中点M，如图2所示，探究：三角板沿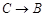方向平移的距离为___________；
（2）操作2：在（1）的情况下，将三角板BC的中点M顺时针方向旋转角度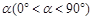
，如图3所示，探究：设三角形板两直角边分别与AB、AC交于点P、Q，观察四边形MPAQ形状的变化，问：四边形MPAQ的面积S是否改变，若不变，求其面积；若改变，试说明理由；
（3）在（2）的情形下，连PQ，设BP=x，记△MPQ的面积为y，试求y关于x的函数关系式，并求x为何值时，y的值是四边形MPAQ的面积的一半，此时，指出四边形MPAQ的形状．
如图，正方形ABCD的长为1， 点E是AD边上的动点且从点A沿AD向D运动， 以BE为边，在BE的上方作正方形BEFG，为DC与EF的交点，请探索：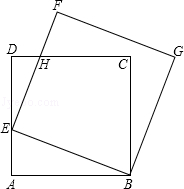
（1）连接CG，线段AE与CG是否相等? 请说明理由.
（2）设AE=x， CG=y， 请确定y与x的函数关系式并说明自变量的取值范围.
（3）连接BH， 当点E运动到边AD上的某一点时将有△BEH∽△BAE，请你指出这一点的位置，并说明理由.