如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示.有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,求在0~4s时间内电阻R上产生的焦耳热.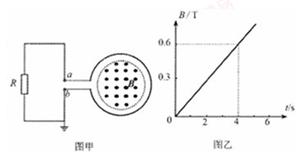
某课外小组经长期观测,发现靠近某行星周围有众多卫星,且相对均匀地分布于行星周围,假设所有卫星绕该行星的运动都是匀速圆周运动,通过天文观测,测得离行星最近的一颗卫星的运动半径为R1,周期为T1,已知万有引力常为G。求:
⑴行星的质量;
⑵若行星的半径为R,行星的第一宇宙速度;
⑶通过天文观测,发现离行星很远处还有一颗卫星,其运动半径为R2,周期为T2,试估算靠近行星周围众多卫星的总质量。
如图所示,半径为R,内径很小的光滑半圆管竖直放置。两个质量均为m的小球a、b以不同的速度进入管内,a通过最高点c时,对管上部的压力为3mg,b通过最高点c时,对管下部的压力为0.75mg。求a,b两球落地点间的距离。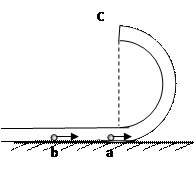
为了研究太阳演化进程,需知道目前太阳的质量M。已知地球半径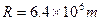 ,地球质量
,地球质量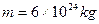 ,日地中心距离
,日地中心距离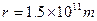 ,地球表面处的重力加速度
,地球表面处的重力加速度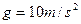 ,地球绕太阳一周所用的时间1年约为
,地球绕太阳一周所用的时间1年约为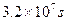 ,试估算目前太阳的质量M(保留一位有效数字,引力常量未知)
,试估算目前太阳的质量M(保留一位有效数字,引力常量未知)
如图,在一圆柱形筒中有一小物体恰能靠在筒壁上随筒一起匀速转动,已知小物体与筒壁间的最大静摩擦力等于正压力的1/4,小物体中心到转轴的距离r=0.3m,求筒转动的角速度ω。(g取10m/s2)
某部队进行军事演习,一架轰炸机在距离地面2000m得高空以250m/s的速度沿水平方向飞行,某时刻相对飞机由静止释放一颗炸弹,则炸弹落地点与释放点水平距离为多少?(不计空气阻力,g=10m/s2)