如图甲所示,有一磁感应强度大小为B、垂直纸面向外的匀强磁场,磁场边界OP与水平方向夹角为θ=45°,紧靠磁场右上边界放置长为L、间距为d的平行金属板M、N,磁场边界上的O点与N板在同一水平面上,O1、O2为电场左右边界中点。在两板间存在如图乙所示的交变电场(取竖直向下为正方向)。某时刻从O点竖直向上以不同初速度同时发射两个相同的质量为m、电量为+q的粒子a和b。结果粒子a恰从O1点水平进入板间电场运动,由电场中的O2点射出;粒子b恰好从M板左端边缘水平进入电场。不计粒子重力和粒子间相互作用,电场周期T未知。求:
(1)粒子a、b从磁场边界射出时的速度va、vb;
(2)粒子a从O点进入磁场到O2点射出电场运动的总时间t;
(3)如果金属板间交变电场的周期 ,粒子b从图乙中t=0时刻进入电场,要使粒子b能够穿出板间电场时E0满足的条件。
,粒子b从图乙中t=0时刻进入电场,要使粒子b能够穿出板间电场时E0满足的条件。
如图所示为四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用。一架质量m="2" kg的无人机,其动力系统所能提供的最大升力F="36" N,运动过程中所受空气阻力大小恒为f="4" N。g取10 m/s2。
(1)无人机在地面上从静止开始,以最大升力竖直向上起飞。求在t="5" s时离地面的高度h;
(2)当无人机悬停在距离地面高度H="100" m处,由于动力设备故障,无人机突然失去升力而坠落。求无人机坠落地面时的速度v;
(3)在无人机坠落过程中,在遥控设备的干预下,动力设备重新启动提供向上最大升力。为保证安全着地,求飞行器从开始下落到恢复升力的最长时间t1
如图所示,光滑平台上有两个刚性小球A和B,质量分别为2m和3m,小球A以速度v0向右运动并与静止的小球B发生碰撞(碰撞过程不损失机械能),小球B飞出平台后经时间t刚好掉入装有沙子向左运动的小车中,小车与沙子的总质量为m,速度为2v0,小车行驶的路面近似看做是光滑的,求: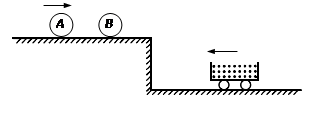
(1)碰撞后小球A和小球B的速度;
(2)小球B掉入小车后的速度。
如图所示,一列沿x轴正方向传播的简谐横波在t=0时刻的波形如图中的实线所示,此时这列波恰好传播到P点,且再经过1.2s,坐标为x=8m的Q点开始起振,求:
①该列波的周期T;
②从t=0时刻到Q点第一次达到波峰时,振源O点相对平衡位置的位移y及其所经过的路程s.
如图甲,真空中竖直放置两块相距为d的平行金属板P、Q,两板间加上如图乙最大值为U0的周期性变化的电压,在Q板右侧某个区域内存在磁感应强度大小为B、方向垂直于纸面向里的有界匀强磁场.在紧靠P板处有一粒子源A,自t=0开始连续释放初速不计的粒子,经一段时间从Q板小孔O射入磁场,然后射出磁场,射出时所有粒子的速度方向均竖直向上.已知电场变化周期T= ,粒子质量为m,电荷量为+q,不计粒子重力及相互间的作用力。求:
,粒子质量为m,电荷量为+q,不计粒子重力及相互间的作用力。求:
(1)t=0时刻释放的粒子在P、Q间运动的时间;
(2)粒子射入磁场时的最大速率和最小速率;
(3)有界磁场区域的最小面积。
如图所示,传送带A、B间距离L=5 m且在同一水平面内,两个轮子半径均为r=0.2 m,半径R=0.4 m的固定竖直光滑圆轨道与传送带相切于B点,C点是圆轨道的最高点.当传送带静止不动时,质量m=1 kg的小煤块在A点以初速度v0=2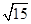 m/s开始运动,刚好能运动到C点.重力加速度g=10 m/s2.求:
m/s开始运动,刚好能运动到C点.重力加速度g=10 m/s2.求: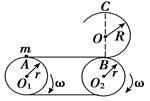
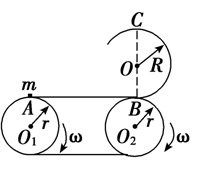
(1)当传送带的轮子以ω=10 rad/s的角速度匀速转动时,将小煤块无初速地放到传送带上的A点,求小煤块从A点运动到B点的过程中在传送带上划过痕迹的长度?
(2)当传送带的轮子匀速转动的角速度在什么范围内时,将小煤块无初速地放到传送带上的A点,小煤块运动到C点时对圆轨道的压力最大,最大压力FC是多大?