(本小题满分14分)在平面直角坐标系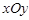 中,椭圆
中,椭圆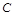 的焦点为
的焦点为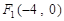 、
、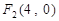 ,且经过点
,且经过点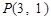 .
.
(1)求椭圆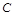 的标准方程;
的标准方程;
(2)若点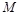 在椭圆
在椭圆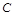 上,且
上,且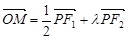 ,求
,求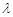 的值.
的值.
(本小题满分12分)某农户建造一间背面靠墙的小房,已知墙面与地面垂直,房屋所占地面是面积为12 m2的矩形,房屋正面每平方米的造价为1200元,房屋侧面每平方米的造价为800元,屋顶的造价为5200元.如果墙高为3 m,且不计房屋背面和地面的费用,问怎样设计房屋能使总造价最低?最低总造价是多少?
(本小题满分14分)设数列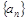 、
、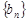 满足:
满足: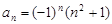 ,
,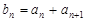 ,
,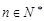 .
.
(1)求 的值;
的值;
(2)求数列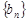 的通项公式;
的通项公式;
(3)求数列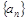 的前
的前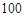 项和
项和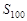 的值.
的值.
(本小题满分14分)如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A、B的一点.
(1)求证:平面PAC⊥平面PBC;
(2)若PA=AB=2,∠ABC=30°,求三棱锥P-ABC的体积.
(本小题满分12分)已知函数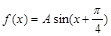 ,
, 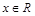 ,且
,且 .
.
(1)求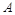 的值;
的值;
(2)若 ,
, 是第二象限角,求
是第二象限角,求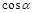 .
.