(本题8分)市某中学开展以“三创一办”为中心,以“校园文明”为主题的手抄报比赛.同学们积极参与,参赛同学每人交了一份得意作品,所有参赛作品均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,将获奖结果绘制成如下两幅统计图.请你根据图中所给信息解答下列问题:
(1)一等奖所占的百分比是__________.
(2)在此次比赛中,一共收到多少份参赛作品?请将条形统计图补充完整.
(3)获三等奖的学生有多少人?
如图,∠B=42°,∠A+10°=∠1,∠ACD=64°,证明AB∥CD.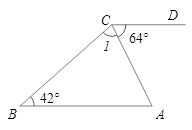
某次七年级数学竞赛共有20道题,每一题答对得10分,答错或不答都扣5分,小明得分要超过100分,他答错与不答题的总数至多不超过多少道题?
在方格纸上,每个小格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.如图在4×4的方格纸上以AB为边的格点△ABC的面积为2个平方单位,完成下列问题: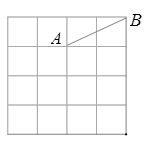
(1)符合条件的C点共有个;
(2)在所给的方面格纸上画出所有以AB为边面积为2个平方面单位的格点三角形(三角形另一个顶点用C1、C2、C3…标记).
解方程组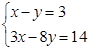
如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,证明∠BAC>∠B.