中子星是恒星演化过程的一种可能结果,它的密度很大。现有一中子星,观测到它的自转周期为T=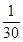 s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67
s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67 10
10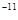 m
m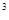 /kg.s
/kg.s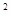 )
)
如图所示,两足够长平行光滑的金属导轨MN、PQ相距为L,导轨平面与水平面夹角α=30°,导轨上端跨接一定值电阻R,导轨电阻不计.整个装置处于方向竖直向上的匀强磁场中,长为L的金属棒cd垂直于MN、PQ放置在导轨上,且与导轨保持电接触良好,金属棒的质量为m、电阻为r,重力加速度为g,现将金属棒由静止释放,当金属棒沿导轨下滑距离为s时,速度达到最大值vm.求: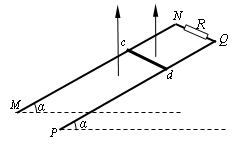
(1)金属棒开 始运动时的加速度大小;
始运动时的加速度大小;
(2)匀强磁场的磁感应强度大小 ;
;
(3)金属棒沿导轨下滑距离为s的过程中,电阻R上产生的电热.
某小型发电站的发电机输出交流电压为500 V,输出电功率为50 kW,用电阻为3 Ω的输 电线向远处用户送电,要求输电线上损失的电功率是输送功率的0.6%,发电站要安装一个升压变压器,到达用户前再用降压变压器变为220 V供用户使用,不考虑变压器的能量损失,求①输电线上输送电流 ②两个变压器原、副线圈的匝数比各是多少?
电线向远处用户送电,要求输电线上损失的电功率是输送功率的0.6%,发电站要安装一个升压变压器,到达用户前再用降压变压器变为220 V供用户使用,不考虑变压器的能量损失,求①输电线上输送电流 ②两个变压器原、副线圈的匝数比各是多少?
同学家新买了一台双门电冰箱,冷藏室容积107L,冷冻室容积118L,假设室内气体为理想气体。
(1)若室内空气摩尔体积为22.5×10-3 m3/mol,在家中关闭冰箱密封门后,电冰箱的冷藏室和冷冻室内大约共有多少个空气分子?
m3/mol,在家中关闭冰箱密封门后,电冰箱的冷藏室和冷冻室内大约共有多少个空气分子?
(2)若室内温度为270C,大气压强为1×105Pa,关 闭冰箱密封门通电一段时间后,冷藏室温度降为60C,冷冻室温度降为-90C,此时冷藏室与冷冻室中空气压强差多大?
闭冰箱密封门通电一段时间后,冷藏室温度降为60C,冷冻室温度降为-90C,此时冷藏室与冷冻室中空气压强差多大?
如图14甲所示,光滑的平行水平金属导轨 、
、 相距
相距 ,
,
在 点和
点和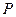 点间连接一个阻值为
点间连接一个阻值为 的电阻,在两导轨间
的电阻,在两导轨间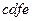 矩形区域内有垂直导轨平面竖直向上、宽为
矩形区域内有垂直导轨平面竖直向上、宽为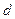 的匀强磁场,磁感应强度为
的匀强磁场,磁感应强度为 。一质量为
。一质量为 、电阻为
、电阻为 、长度也刚好为
、长度也刚好为 的导体棒
的导体棒 垂直搁在导轨上,与磁场左边界相距
垂直搁在导轨上,与磁场左边界相距 。现用一个水平向右的力
。现用一个水平向右的力 拉棒
拉棒 ,使它由静止开始运动,棒
,使它由静止开始运动,棒 离开磁场前已做匀速直线运动,棒
离开磁场前已做匀速直线运动,棒 与导轨始终保持良好接触,导轨电阻不计,
与导轨始终保持良好接触,导轨电阻不计, 随
随 与初始位置的距离
与初始位置的距离 变化的情况如图14乙,
变化的情况如图14乙, 已知。求:
已知。求: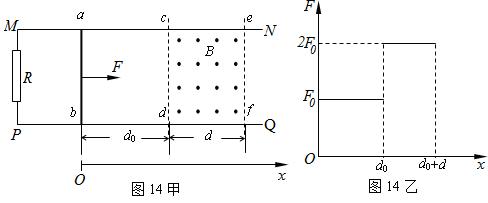
(1)棒 离开磁场右边界时的速度;
离开磁场右边界时的速度;
(2)棒 通过磁场区域的过程中整个回路所消耗的电能;
通过磁场区域的过程中整个回路所消耗的电能;
(3)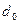 满足什么条件时,棒
满足什么条件时,棒 进入磁场后一直做匀速运动。
进入磁场后一直做匀速运动。
如图13所示,有一磁感强度 的水平匀强磁场,垂直放置一很长的金属框架,框架上有一导体
的水平匀强磁场,垂直放置一很长的金属框架,框架上有一导体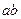 与框架边垂直且始终保持良好接触,由静止开始下滑。已知框架的宽度为
与框架边垂直且始终保持良好接触,由静止开始下滑。已知框架的宽度为 ,质量为
,质量为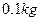 ,电阻为
,电阻为 ,框架电阻不计,取
,框架电阻不计,取 ,求:
,求:
(1) 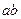 中电流的方向如何?
中电流的方向如何?
(2)导体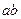 下落的最大速度;
下落的最大速度;
(3)导体 在最大速度时的电功率。
在最大速度时的电功率。