(本小题满分14分)已知函数 .
.
(1)讨论 的单调区间;
的单调区间;
(2)若函数 在[
在[ ,3]上有三个零点,求实数m的取值范围;
,3]上有三个零点,求实数m的取值范围;
(3)设函数 (e为自然对数的底数),如果对任意的
(e为自然对数的底数),如果对任意的 ,都有
,都有 恒成立,求实数n的取值范围.
恒成立,求实数n的取值范围.
已知数列 的前
的前 项和为
项和为 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列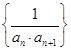 的前
的前 项和
项和 的取值范围.
的取值范围.
已知等比数列 中
中 ,数列
,数列 满足
满足 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
平面直角坐标系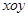 中,直线
中,直线 的参数方程
的参数方程 (
( 为参数),圆
为参数),圆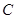 的方程为
的方程为 ,以坐标原点
,以坐标原点 为极点,
为极点,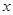 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求直线 和圆
和圆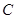 的极坐标方程;
的极坐标方程;
(2)求直线 和圆
和圆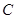 的交点的极坐标(要求极角
的交点的极坐标(要求极角 ).
).
已知函数 ,
, .
.
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)设函数 ,求函数
,求函数 的单调区间;
的单调区间;
(3)若在 上存在一点
上存在一点 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
如图,已知长方形 中,
中,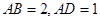 ,
,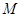 为
为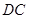 的中点,将
的中点,将 沿
沿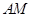 折起,使得平面
折起,使得平面
 平面
平面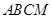 .
.
(1)求证: ;
;
(2)若点 是线段
是线段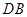 上的一动点,问点
上的一动点,问点 在何位置时,二面角
在何位置时,二面角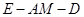 的余弦值为
的余弦值为 .
.