如图所示是一个透明圆柱体的横截面，一束单色光平行于直径AB射向圆柱体，光线经过折射后恰能射到B点。已知透明介质对单色光的折射率为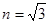
，横截面的半径为R，光在真空中的传播速度为c，求：①光在介质中运动的时间；
②平行光线到直径AB的距离d。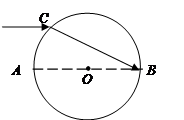
一滑雪人与滑雪板的总质量为60kg，从长为100m、倾角为30°的斜坡顶端由静止开始匀加速下滑，经10s滑到了坡底。取g=10m/s2，求：
滑雪人下滑的加速度；
人与滑雪板所受的阻力（包括摩擦和空气阻力）
如图所示，轻绳悬挂一质量为m=2.0kg的小球，现对小球再施加一个力F，使小球静止在绳子与竖直方向成60º的位置上，g取10m/s2。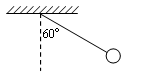
若F为水平方向，求F的大小；
若要使F的取值最小，求F的大小和方向。
汽车以v0=10m/s的速度在水平路面上匀速运动，刹车后经2秒速度变为6m/s，求：刹车过程中的加速度；
刹车后6秒内的位移；
汽车在运动最后2秒内发生的位移。.
如图所示，在倾角θ＝37°的足够长的固定的斜面底端有一质量m＝1.0kg的物体．物体与斜面间动摩擦因数µ＝0.25，现用轻细绳将物体由静止沿斜面向上拉动．拉力F＝10N，方向平行斜面向上．经时间t＝4s绳子突然断了，求：
绳断时物体的速度大小．
从绳子断了开始到物体再返回到斜面底端的运动时间．（sin37°＝0.60 cos37°＝0.80，g＝10m/s2）
如图，质量为10 kg的物体，与水平面间的动摩擦因数μ = 0.1。当受到50 N、与水平方向成37° 角的拉力F的作用时，物体由静止开始沿水平面做直线运动。求
经过2s后，物体运动的速度？
经过2s后，物体
运动了多远？（sin37°＝0.60 ,cos37°＝0.80，g＝10m/s2）