【原题】如图所示，带电平行金属板相距为2R，在两板间半径为R的圆形区域内有垂直纸面向里的匀强磁场，磁感应强度为B，两板及其左侧边缘连线均与磁场边界刚好相切。一质子（不计重力）沿两板间中心线O1O2从左侧O1点以某一速度射入，沿直线通过圆形磁场区域，然后恰好从极板边缘飞出，在极板间运动时间为t0。若仅撤去磁场，质子仍从O1点以相同速度射入，经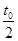
时间打到极板上。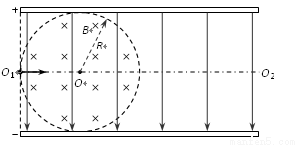
⑴求两极板间电压U；
⑵求质子从极板间飞出时的速度大小；
⑶若两极板不带电，保持磁场不变，质子仍沿中心线O1 O2从O1点射入，欲使质子从两板左侧间飞出，射入的速度应满足什么条件？
宇航员站在一星球表面上的某高处，沿水平方向抛出一个小球，经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L.若抛出时的初速度增大为原来的2倍，则抛出点与落地点之间的距离为
L.已知两落地点在同一水平面上，该星球的半径为R，万有引力常量为G，求该星球的质量M.
荡秋千是大家喜爱的一项体育活动.随着科技的迅速发展，将来的某一天，同学们也许会在其他星球上享受荡秋千的乐趣.假设你当时所在星球的质量是M、半径为R,可将人视为质点，秋千质量不计、摆长不变、摆角小于90°，万有引力常量为G.那么，
（1）该星球表面附近的重力加速度g星等于多少？
（2）若经过最低位置的速度为v0,你能上升的最大高度是多少？
月球质量是地球质量的
，月球的半径是地球半径的
.月球上空高500 m处有一质量为60 kg的物体自由下落.(1)它落到月球表面所需要的时间是多少?(2)它在月球上的重力和质量跟在地球上有没有不同(g地="9.8" m/s2)?
飞船沿半径为R的圆周绕地球运动，如图所示，其周期为T,如果飞船要返回地面，可在轨道上某一点A处将速率降低到适当数值，从而使飞船沿着以地心为焦点的椭圆轨道运行，椭圆和地球表面相切于B点，设地球半径为R0，问飞船从A点返回到地面上B点所需时间为多少？
月球环绕地球运动的轨道半径约为地球半径的60倍，运行周期约为27天，试用开普勒定律计算出：在赤道平面内离地面多大高度，人造地球卫星可以随地球一起转动，就像停留在天空不动一样.（地球半径约为6.4×103 m）