如下图所示,弹簧左端固定,右端被一个小球恰好压缩在光滑水平桌面上,已知小球质量为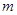 ,桌面水平高度为
,桌面水平高度为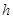 ,小球释放后,在弹簧弹力作用下水平向右飞出,弹簧原长恰好在桌面边沿。记录下小球落点P。
,小球释放后,在弹簧弹力作用下水平向右飞出,弹簧原长恰好在桌面边沿。记录下小球落点P。
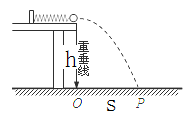
(1)若测得某次压缩弹簧释放后小球落点P痕迹到O点的距离为s,则释放小球前弹簧的弹性势能表达式为 ;
(2)该同学改变弹簧的压缩量进行多次测量得到下表一组数据:

结合(1)问与表中数据,可分析得到弹簧弹性势能Ep与弹簧压缩量x之间的函数关系式为 (k为比例系数)
A.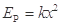 |
B.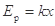 |
C.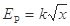 |
D.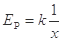 |
(3)你认为Ep与x的关系式中的比例系数k与弹簧的什么因素有关?
如图所示,在光滑绝缘水平面上有两个带电小球 、
、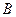 ,质量分别为3m和m,小球
,质量分别为3m和m,小球 带正电q,小球
带正电q,小球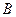 带负电-2q,开始时两小球相距s0,小球
带负电-2q,开始时两小球相距s0,小球 有一个水平向右的初速度v0,小球
有一个水平向右的初速度v0,小球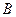 的初速度为零,若取初始状态下两小球构成的系统的电势能为零,
的初速度为零,若取初始状态下两小球构成的系统的电势能为零,
(1)试证明:当两小球的速度相同时系统的电势能最大,并求出该最大值;
(2)在两小球的间距仍不小于s0的运动过程中,求出系统的电势能与系统的动能的比值的取值范围。
如图所示,一水平光滑、距地面高为h、边长为a的正方形MNPQ桌面上,用长为L的不可伸长的轻绳连接质量分别为mA、mB的A、B两小球,两小球在绳子拉力的作用下,绕绳子上的某点O以不同的线速度做匀速圆周运动,圆心O与桌面中心重合,已知mA=0.5 kg,L=1.2 m,LAO=0.8 m,a=2.1 m,h=1.25 m,A球的速度大小vA=0.4 m/s,重力加速度g取10 m/s2,求:
(1)绳子上的拉力F以及B球的质量mB;
(2)若当绳子与MN平行时突然断开,则经过1.5 s两球的水平距离;
(3)两小球落至地面时,落点间的距离.
如图所示,高h=0.8m的绝缘水平桌面上方的区域Ⅰ中存在匀强电场,场强E的方向与区域的某一边界平行,区域Ⅱ中存在垂直于纸面的匀强磁场B。现有一质量m=0.01kg,带电荷量q=+10-5C的小球从A点以v0=4m/s的初速度水平向右运动,匀速通过区域Ⅱ后落在水平地面上的B点,已知:小球与水平桌面间的动摩擦因数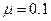 ,L=1m,h=0.8m,x=0.8m,取g=10m/s2。试求:
,L=1m,h=0.8m,x=0.8m,取g=10m/s2。试求:
(1)小球在区域Ⅱ中的速度;
(2)区域Ⅱ中磁感应强度B的大小及方向;
(3)区域Ⅰ中电场强度E的大小及方向。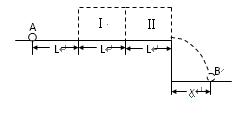
如图,粗糙水平面与半径R=2m的光滑 圆弧轨道相切于C点。静止于A处的物体,在大小为10N、方向与水平面成37°角的拉力F作用下沿水平面运动,到达C点时立即撤去F,物体沿光滑圆弧向上冲,然后返回经过C点进入水平面且停在B处。已知:物体返回经过C点时对轨道压力大小为物体重量的2.8倍,sAC=15m,sBC=4.5m,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
圆弧轨道相切于C点。静止于A处的物体,在大小为10N、方向与水平面成37°角的拉力F作用下沿水平面运动,到达C点时立即撤去F,物体沿光滑圆弧向上冲,然后返回经过C点进入水平面且停在B处。已知:物体返回经过C点时对轨道压力大小为物体重量的2.8倍,sAC=15m,sBC=4.5m,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
(1)物体的质量
(2)物体与水平面的动摩擦因素
(1)图为某介质中一列简谐横波的图像, a、b、为该波上的质点,已知此时a点正沿y轴正向运动,且在1s内完成5次全振动。
①分析从该时刻起a、b两质点那个先回到平衡位确置;
②定波的传播方向和波速。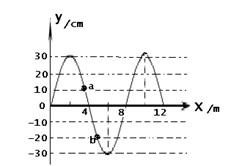
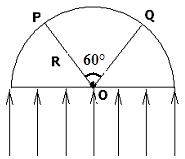
(2)平行光A垂直射向一半径为R的玻璃半球的平面,其截面如图所示。发现只有P、Q之间所对应圆心角为600的球面上有光线射出,则:
①玻璃对光线的折射率
②若仅将平行光A换成B平行光,测得有光线射出的范围增大。设A、B两种光在玻璃球中的速度分别为vA、vB,试比较vA、vB的大小关系