已知双曲线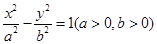 ,
, ,
,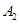 是实轴顶点,
是实轴顶点, 是右焦点,
是右焦点,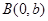 是虚轴端点,若在线段
是虚轴端点,若在线段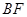 上(不含端点)存在不同的两点
上(不含端点)存在不同的两点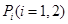 使得
使得
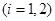 构成以
构成以 为斜边的直角三角形,则双曲线离心率
为斜边的直角三角形,则双曲线离心率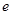 的取值范围是( )
的取值范围是( )
A.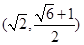 |
B.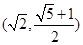 |
C. |
D.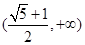 |
设函数fn(x)=n2x2(1-x)n(n为正整数),则fn(x)在[0,1]上的最大值为( )
| A.0 | B.1 | C.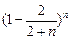 |
D.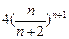 |
设f(x)可导,且f′(0)=0,又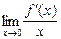 =-1,则f(0)( )
=-1,则f(0)( )
| A.可能不是f(x)的极值 | B.一定是f(x)的极值 |
| C.一定是f(x)的极小值 | D.等于0 |
经过原点且与曲线y= 相切的方程是( )
相切的方程是( )
A.x+y=0或 +y="0" +y="0" |
B.x-y=0或 +y=0 +y=0 |
C.x+y=0或 -y="0" -y="0" |
D.x-y=0或 -y=0 -y=0 |
y=esinxcos(sinx),则y′(0)等于( )
| A.0 | B.1 | C.-1 | D.2 |
设f(x)=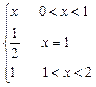 则f(x)的连续区间为( )
则f(x)的连续区间为( )
| A.(0,2) | B.(0,1) | C.(0,1)∪(1,2) | D.(1,2) |