抛物线y2=-8x中,以(-1,1)为中点的弦的方程是( )
| A.x-4y-3="0" | B.x+4y+3=0 |
| C.4x+6y-3="0" | D.4x+y+3=0 |
对于抛物线y2=4x上任意一点Q,点P(a,0)都满足|PQ|≥|a|,则a的取值范围是( )
| A.(-∞,0) | B.(-∞,2] | C.[0,2] | D.(0,2) |
顶点在原点,焦点在x轴上的抛物线被直线y=x-2截得的线段长为4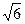 ,求抛物线的方程.
,求抛物线的方程.
过抛物线y2=4x的顶点O作两条互相垂直的直线分别交抛物线于A、B两点,则线段AB的中点P(x,y)的轨迹方程是( )
A.y2="-2x-8" B.y2=2x-8
C.y2="2x+8" D.y2=-2x+8
设坐标原点为O,抛物线y2=2x与过焦点的直线交于A、B两点,则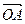 ·
· 等于( )
等于( )
A.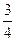 B.-
B.-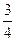 C.3 D.-3
C.3 D.-3