(本小题满分10分,坐标系与参数方程选讲)
己知在平面直角坐标系 中,圆
中,圆 的参数方程为
的参数方程为 (
( 为参数).以原点
为参数).以原点 为极点,以
为极点,以 轴的非负半轴为极轴的极坐标系中,直线
轴的非负半轴为极轴的极坐标系中,直线 的极坐标方程为
的极坐标方程为 ,直线
,直线 与圆
与圆 相交于
相交于 两点,求弦
两点,求弦 的长.
的长.
(满分12分)已知 (Ⅰ)判断
(Ⅰ)判断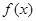 的奇偶性;(Ⅱ)求
的奇偶性;(Ⅱ)求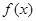 的值域.
的值域.
(满分12分)计算:(Ⅰ) 
(Ⅱ)已知 (其值用
(其值用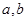 表示)
表示)
(本小题满分16分)已知数列 的前
的前 项和
项和 满足:
满足: ,数列
,数列 满足:对任意
满足:对任意 有
有
 .
.
(1)求数列 与数列
与数列 的通项公式;
的通项公式;
(2)记 ,数列
,数列 的前
的前 项和为
项和为 ,证明:当
,证明:当 时,
时, .
.
(本小题满分16分)如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植甲水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的 处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是
处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是 ,点
,点 在直径
在直径 上,且
上,且 .
.
(1)若 ,求
,求 的长;
的长;
(2)设 , 求该空地产生最大经济价值时种植甲种水果的面积.
, 求该空地产生最大经济价值时种植甲种水果的面积.
(本小题满分16分)对于函数 ,如果存在实数
,如果存在实数 使得
使得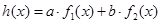 ,那么称
,那么称 为
为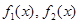 的生成函数.
的生成函数.
(1)下面给出两组函数, 是否分别为
是否分别为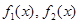 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组: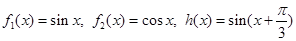 ;
;
第二组: ;
;
(2)设 ,生成函数
,生成函数 .若不等式
.若不等式 在
在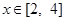 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.