(本小题满分12分)某大学准备在开学时举行一次大学一年级学生座谈会,拟邀请 名来自本校机械工程学院、海洋学院、医学院、经济学院的学生参加,各学院邀请的学生数如下表所示:
名来自本校机械工程学院、海洋学院、医学院、经济学院的学生参加,各学院邀请的学生数如下表所示:
| 学院 |
机械工程学院 |
海洋学院 |
医学院 |
经济学院 |
| 人数 |
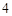 |
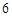 |
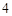 |
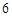 |
(Ⅰ)从这 名学生中随机选出
名学生中随机选出 名学生发言,求这
名学生发言,求这 名学生中任意两个均不属于同一学院的概率;
名学生中任意两个均不属于同一学院的概率;
(Ⅱ)从这 名学生中随机选出
名学生中随机选出 名学生发言,设来自医学院的学生数为
名学生发言,设来自医学院的学生数为 ,求随机变量
,求随机变量 的概率分布列和数学期望.
的概率分布列和数学期望.
(本小题12分)已知不等式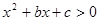 的解集为
的解集为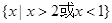
(1)求b和c的值; (2)求不等式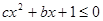 的解集.
的解集.
(本小题满分12分)
已知函数 在
在 上是增函数,在
上是增函数,在 上是减函数.
上是减函数.
(1)求函数 的解析式;
的解析式;
(2)若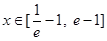 时,
时,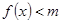 恒成立,求实数
恒成立,求实数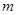 的取值范围;
的取值范围;
(3)是否存在实数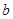 ,使得方程
,使得方程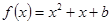 在区间
在区间 上恰有两个相异实数根,若存在,求出
上恰有两个相异实数根,若存在,求出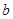 的范围,若不存在说明理由.
的范围,若不存在说明理由.
(本小题满分12分)
已知 ,解不等式
,解不等式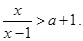
(本小题满分12分)
设平面直角坐标系 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个交点,经过这三个交点的圆记为
的图象与两坐标轴有三个交点,经过这三个交点的圆记为 .求:
.求:
(Ⅰ)求实数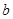 的取值范围;
的取值范围;
(Ⅱ)求圆 的方程;
的方程;
(Ⅲ)问圆 是否经过某定点(其坐标与b 无关)?请证明你的结论.
是否经过某定点(其坐标与b 无关)?请证明你的结论.
(本小题满分12分)
等比数列{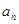 }的前
}的前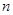 项和为
项和为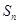 ,已知对任意的
,已知对任意的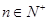 ,点
,点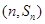 均在函数
均在函数 且
且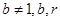 均为常数)的图像上.
均为常数)的图像上.
(1)求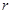 的值;
的值;
(2)当 时,记
时,记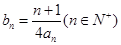 ,求数列
,求数列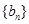 的前
的前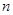 项和
项和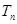 .
.