如图所示,椭圆C: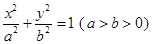 的两个焦点为
的两个焦点为 、
、 ,短轴两个端点为
,短轴两个端点为 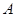 、
、 .已知
.已知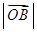 、
、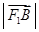 、
、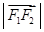 成等比数列,
成等比数列,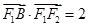 ,与
,与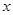 轴不垂直的直线
轴不垂直的直线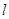 与 C 交于不同的两点
与 C 交于不同的两点 、
、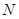 ,记直线
,记直线 、
、 的斜率分别为
的斜率分别为 、
、 ,且
,且 .
.
(Ⅰ)求椭圆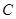 的方程;
的方程;
(Ⅱ)求证直线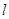 与
与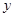 轴相交于定点,并求出定点坐标;
轴相交于定点,并求出定点坐标;
(Ⅲ)当弦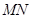 的中点
的中点 落在四边形
落在四边形 内(包括边界)时,求直线
内(包括边界)时,求直线 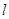 的斜率的取值范围.
的斜率的取值范围.
(本小题满分12分) 已知二次函数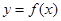 ,当
,当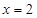 时函数取最小值
时函数取最小值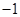 ,且
,且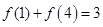 .
.
(1) 求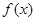 的解析式;
的解析式;
(2) 若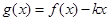 在区间
在区间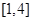 上不单调,求实数
上不单调,求实数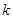 的取值范围。
的取值范围。
(本小题满分12分)求下列函数值域
(1)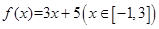
(2)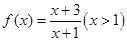
(本小题满分10分) 设集合 ,
, .
.
(1)若 ,判断集合
,判断集合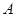 与
与 的关系;
的关系;
(2)若 ,求实数
,求实数 组成的集合
组成的集合 .
.
(本小题满分12分)设A(x1,y1),B(x2,y2)是函数f(x)= 的图象上任意两点,且
的图象上任意两点,且 ,已知点M的横坐标为
,已知点M的横坐标为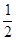 .
.
求证:M点的纵坐标为定值;
若Sn=f( ∈N*,且n≥2,求Sn;
∈N*,且n≥2,求Sn;
已知an= ,其中n∈N*.
,其中n∈N*.
Tn为数列{an}的前n项和,若Tn<λ(Sn+1+1)对一切n∈N*都成立,试求λ的取值范围.
(本小题满分12分)设{an}是公比为 q的等比数列,且a1,a3,a2成等差数列.
(1)求q的值;
(2)设{bn}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.