如图所示，一质量为m=0.5kg，电荷量为q=+0.2C的小物块（可视为质点），放在离地面高度为h=5m的水平放置、厚度不计的绝缘圆盘边缘，并随圆盘一起绕中心转轴顺时针做匀速圆周运动，圆盘的角速度为ω=2rad/s，半径为r=1m，圆盘和小物块之间的动摩擦因数为μ=0.5。以圆盘左侧垂直于纸面的切面和过圆盘圆心O点与空间中A点的竖直平面为界（两平面平行），将空间分为Ⅰ、Ⅱ、Ⅲ三个空间区域，当小物块转动时，Ⅰ区域出现随时间均匀增大的电场E（图中未画出），电场方向是竖直方向。当E增大到E1时，小物块刚好从空间中的A点离开圆盘，且垂直于Ⅰ、Ⅱ区域边界进入Ⅱ区域，此时，Ⅱ区域和Ⅲ区域立即出现一竖直向上的匀强电场E2（图中未画出），E2=25N/C，且Ⅲ区域有一垂直于纸面向里的匀强磁场，磁场宽度为L=4m，g=10m/s2。求：
（1）E1的大小和方向；
（2）若小物块在磁场宽度范围内落地，则磁感应强度B的取值范围是多少？
（3）现将磁感应强度B取某一值，当小物块离开A后一小段时间，紧贴圆盘圆心O点下方以速度v0=
m/s水平抛出一木制小球，最终两者在磁场宽度范围内的地面上相遇，则从小物块离开A点时开始计时，抛出木制小球的时刻t为多少？
设有一条小河，其宽度H=800m，河水匀速流动，且流速v1=2m/s，汽船在静水中的速度v2=4m/s。如果汽船的速度始终保持与河岸垂直，试求当船到达对岸时，汽船沿水流方向运动了多远？
如图所示，一根粗细均匀、内壁光滑、竖直放置的玻璃管下
端密封，上端封闭但留有一抽气孔。管内下部被活塞封住一定量的气体（可视为理
想气体），气体温度为T1.开始时，将活塞上方的气体缓慢抽出，当活塞上方的压强
达到p0时，活塞下方气体的体积为V1，活塞上方玻璃管的容积为2.6V1.活塞因重力
而产生的压强为0.5p0.继续将活塞上方抽成真空并密封。整个抽气过程中管内气体
温度始终保持不变。然后将密封的气体缓慢加热。求：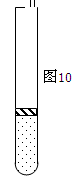
①活塞刚碰到玻璃管顶部时气体的温度；
②当气体温度达到1.8T1时气体的压强．
如图所示，竖直放置的汽缸内壁光滑，活塞厚度与质量均不
计，在B处设有限制装置，使活塞只能在B以上运动，B以下汽缸的容积为V0，A、
B之间的容积为0.2V0；开始时活塞在A处，温度为87°C，大气压强为p0，现缓慢降
低汽缸内气体的温度，直至活塞移动到A、B的正中间，然后保持温度不变，在活塞
上缓慢加沙，直至活塞刚好移动到B，然后再缓慢降低汽缸内气体的温度，直到-3°C。求：
（1）活塞刚到达B处时的温度TB；
（2）缸内气体最后的压强p；
如图所示，长31cm内径均匀的细玻璃管，开口向下竖直放置，齐口
水银柱封住10cm长的空气柱，若把玻璃管在竖直平面内缓慢转动90o后至开口端水
平，发现空气长度变为7.2cm。然后继续缓慢转动90o至开口向上。求：
（1）大气压强的值。
（2）末状态时空气柱的长度。
试估算（1）水分子的直径（2）标准状态下气体分子间的平均距离。
（
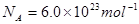）（保留一位有效数字）