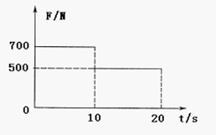
如图,质量分别为m1=1.0kg和m2=2.0kg的弹性小球a、b,用弹性轻绳紧紧的把它们捆在一起,使它们发生微小的形变。该系统以速度v0=0.10m/s沿光滑水平面向右做直线运动。某时刻轻绳突然自动断开,断开后,小球b停止运动、小球a继续沿原直线运动。求:
(i)刚分离时小球a的速度大小v1;
(ii)两球分开过程中释放的弹性势能Ep。
在距某村庄较远的地方修建了一座小型水电站,发电机输出功率为9kW,输出电压为500V,输电线的总电阻为10Ω,允许线路损耗的功率为发电机输出功率的4%,求:
(1)村民和村办小企业需要220V电压时,所用升压变压器和降压变压器的原、副线圈的匝数比各为多少?(不计变压器的损耗)
(2)若不用变压器而由发电机直接输送,村民和村办小企业得到的电压和功率是多少?
如图所示,处于匀强磁场中的两根足够长。电阻不计的平行金属导轨相距1m,导轨平面与水平面成370角,下端连接阻值为R的电阻。匀强磁场方向与导轨平面垂直。质量为0.2kg。电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25。求:
(1)求金属棒沿导轨由静止开始下滑时的加速度大小;
(2)当金属棒下滑速度达到稳定时,电阻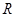 消耗的功率为
消耗的功率为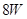 ,求该速度的大小;
,求该速度的大小;
(3)在上问中,若 ,金属棒中的电流方向
,金属棒中的电流方向 到
到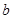 ,求磁感应强度的大小与方向。(
,求磁感应强度的大小与方向。( 取
取 ,
, ,
,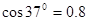 )
)
如图所示,静止在水平地面上的玩具小鸭质量m=0.5kg,受到与水平面夹角为53°的恒定拉力后,玩具开始沿水平地面运动。若拉力F=4.0N,经过时间t=2.0s,玩具移动距离为x=4.8m;撤去拉力F后,玩具又向前滑行一段距离。求:(sin53°=0.8,cos53°=0.6)
⑴运动过程中,玩具的最大速度;
⑵撤去拉力后,玩具继续前进的距离。
“使命行动-2010”跨区机动演习的兰州军区某集团军部队,在川西某高原组织了一场信息化条件下实兵对抗联合火力打击演练。在这次军演中多支特战分队通过机降秘密潜入“敌”后方阵地,对“敌”指挥枢纽进行特种破袭。某一空降特战兵在敌方的上空实施空降, 在飞机悬停空中后,空降特战兵从机舱中一跃而下,把空降特战兵空降假定为如下过程:空降特战兵出飞机舱后先做自由落体运动,下落了2s后,打开伞包匀速运动了4s,接着做匀减速直线运动6s到达了“敌方”的地面,此时空降兵的速度恰好为零,g取10m/s2。 求:
(1)空降特战兵做自由落体运动下落的距离是多少?
(2)空降特战兵实施空降发生的总位移是多少?
质量为50kg的人站在升降机内的体重计上。若升降机上升过程中,体重计的示数F随时间t的变化关系如图所示,g取10m/s2。
(1)求0—10s内升降机的加速度。
(2)10s—20s内升降机做什么运动。