如图所示,平面直角坐标系第一象限存在竖直向上的匀强电场,距离原点O为3a处有一个竖直放置的荧光屏,荧光屏与x轴相交于Q点,且纵贯第四象限。一个顶角等于30°的直角三角形区域内存在垂直平面向里的匀强磁场,三角形区域的一条直角边MN与y轴重合,且MN被x轴垂直平分。已知MN的长度为6a,磁感应强度为B,电子束以相同的速度v0从LO区间垂直y轴和磁场方向射入直角三角形区域。从y= 2a射入磁场的电子运动轨迹恰好经过原点O,假设第一象限的电场强度大小为E=Bv0,试求: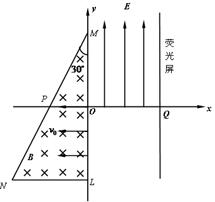
(1)电子的比荷;
(2)电子束从+y轴上射入电场的纵坐标范围;
(3)从磁场中垂直于y轴射入电场的电子打到荧光屏上距Q点的最远距离。
某型号小汽车发动机的额定功率为60 kW,汽车质量为1×103 kg,在水平路面上正常行驶中所受到的阻力为车重的0.15倍,g取10 m/s2.求:此型号汽车在水平路面行驶能达到的最大速度是多少?
若此型号汽车以额定功率加速行驶,当速度达到20 m/s 时的加速度大小是多少?
质量为60 kg的驾驶员驾驶此型号汽车在水平高速公路上以30 m/s的速度匀速行驶,设轮胎与路面的动摩擦因数为0.60,驾驶员的反应时间为0.30 s,则驾驶员驾驶的汽车与前车保持的安全距离最少为多少?
如图所示电子射线管.阴极K发射电子,阳极P和阴极K间 加上电压后电子被加速。A、B是偏向板,使飞进的电子偏离.若已知P、K间所加电压UPK=2.5×103V,两极板长度L=6.0×10-2m,板间距离d=3.6×10-2m,所加电压UAB=1000V,R=3×10-2m, 电子质量me=9.1×10-31kg,电子的电荷量e=-1.6×10-19C。设从阴极出来的电子速度为0,不计重力。 试问:电子通过阳极P板的速度υ0是多少?
电子通过偏转电极时具有动能Ek是多少?
电子过偏转电极后到达距离偏转电极R=3×10-2m荧光屏上 O′点,此点偏离入射方向的距离y是多少?
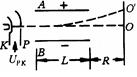
如图所示的电路中已知电源电动势E=36V,内电阻r=2Ω,R1=20Ω,每盏灯额定功率都是2W,额定电压也相同。当K闭合调到R2=14Ω时,两灯都正常发光;当K断开后为使L2仍正常发光,求R2应调到何值?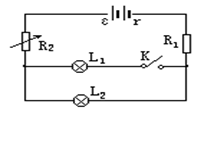
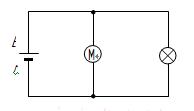
如右图所示,电源电动势E="10" V,内阻r=0.5Ω,标有“8 V,16 W”的灯泡恰好能正常发光,电动机M绕组的电阻R0=1Ω,求:路端电压;
电源的总功率;
电动机的输出功率。
如图所示,电源电动势为10V,内电阻为0.5Ω,R1=5.5Ω,R2=4Ω,当S闭合时,一带电油滴恰好静止在水平放置的平行金属板间。求S断开时,油滴的加速度为多大?方向如何?取g=10