在平面直角坐标系xOy中,对于点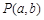 和点
和点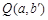 ,给出如下定义:若
,给出如下定义:若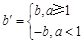 ,则称点
,则称点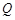 为点
为点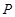 的限变点.例如:点
的限变点.例如:点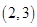 的限变点的坐标是
的限变点的坐标是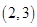 ,点
,点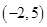 的限变点的坐标是
的限变点的坐标是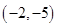 .
.
(1)①点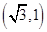 的限变点的坐标是___________;
的限变点的坐标是___________;
②在点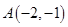 ,
,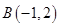 中有一个点是函数
中有一个点是函数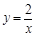 图象上某一个点的限变点,这个点是_______________;
图象上某一个点的限变点,这个点是_______________;
(2)若点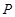 在函数
在函数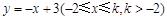 的图象上,其限变点
的图象上,其限变点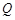 的纵坐标
的纵坐标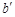 的取值范围是
的取值范围是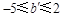 ,求
,求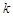 的取值范围;
的取值范围;
(3)若点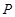 在关于
在关于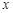 的二次函数
的二次函数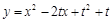 的图象上,其限变点
的图象上,其限变点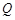 的纵坐标
的纵坐标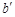 的取值范围是
的取值范围是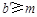 或
或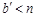 ,其中
,其中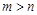 .令
.令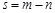 ,求
,求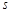 关于
关于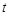 的函数解析式及
的函数解析式及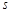 的取值范围.
的取值范围.
(本题11分)如图所示,矩形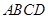 中,
中,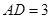 厘米,
厘米, 厘米(
厘米(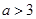 ).动点
).动点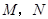 同时从
同时从 点出发,分别沿
点出发,分别沿 ,
,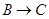 运动,速度是
运动,速度是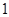 厘米/秒.过
厘米/秒.过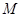 作直线垂直于
作直线垂直于 ,分别交
,分别交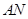 ,
,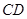 于
于 .当点
.当点 到达终点
到达终点 时,点
时,点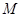 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为 秒.
秒.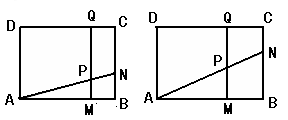
(1)若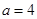 厘米,
厘米,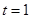 秒,求PM的长度;
秒,求PM的长度;
(2)若 厘米,求出某个时间
厘米,求出某个时间 ,使⊿PNB∽⊿PAD,并求出它们的相似比;
,使⊿PNB∽⊿PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求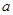 的取值范围;
的取值范围;
(本题8分)2010年中国足球甲级联赛,积分规则如下表:
 |
胜一场 |
平一场 |
负一场 |
| 积分 |
3 |
1 |
0 |
赛季之初,已经降级的成都谢菲联队俱乐部提出本赛季第一阶段比赛目标是:联赛赛进行到第12轮时,球队积分为19分。请通过计算,判断成都谢菲联队胜、平、负各几场才能实现球队的目标?
(本题7分)如图所示,一块三角形的余料,底边BC长1.8米,高AD=1米,要利用它裁剪一个长宽比是3:2的长方形,使长方形的长在BC上,另两个顶点在AB、AC上,求长方形的面积.
如图所示,已知:⊿ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F.
(1)试说明⊿ABD≌⊿BCE.
(2)⊿AEF与⊿BEA相似吗?说说你的理由.
(3)等式 成立吗?请说明理由.
成立吗?请说明理由.
阅读:对于关于 的二次三项式
的二次三项式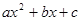 (
(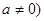 ,当
,当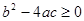 时,
时,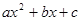 在实数范围内可以分解因式。
在实数范围内可以分解因式。
例:对于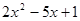 ,因为:
,因为: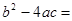
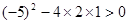 ,所以:
,所以: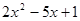 在实数范围内可以分解因式。
在实数范围内可以分解因式。
问题:当m取什么值的时候,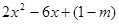 在实数范围内可以分解因式。
在实数范围内可以分解因式。