如图,在矩形ABCD中,AB=6cm,BC=8cm.如果点E由点B出发沿BC方
向向点C匀速运动,同时点F由点D出发沿DA方向向点A匀速运动,它们的速度分别为2cm/s和1cm/s.FQ⊥BC,分别交AC、BC于点P和Q,设运动时间为t(s)(0<t<4).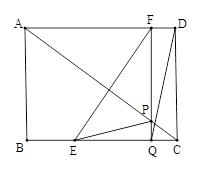
(1)连结EF、DQ,若四边形EQDF为平行四边形,求t的值;
(2)连结EP,设△EPC的面积为ycm2,求y与t的函数关系式,并求y的最大值;
(3)若△EPQ与△ADC相似,请直接写出t的值.
某工厂一种产品2013年的产量是100万件,计划2015年产量达到121万件.假设2013年到2015年这种产品产量的年增长率相同.
(1)求2013年到2015年这种产品产量的年增长率;
(2)2014年这种产品的产量应达到多少万件?
某公司为了了解员工每人所创年利润情况,公司从各部抽取部分员工对每年所创年利润情况进行统计,并绘制如图1,图2统计图.
(1)将图补充完整;
(2)本次共抽取员工 人,每人所创年利润的众数是 ,平均数是 ;
(3)若每人创造年利润10万元及(含10万元)以上为优秀员工,在公司1200员工中有多少可以评为优秀员工?
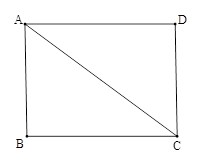
如图,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
如图,从地面上的一点A测得山顶电视发射塔的上端P点的仰角是45°,向前走60m到达B点,测得P点的仰角是60°,电视塔底部Q点的仰角是30°,求电视发射塔PQ的高度。(结果保留根号)
商场计划拨款9万元,从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出场价分别为甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元.在同时购进两种不同型号的电视机的方案中,为使销售时获利最多,该选择哪种进货方案?