某中学计划从办公用品公司购买A,B两种型号的小黑板.经洽谈,购买一块A型小黑板比购买一块B型小黑板多用20元,且购买5块A型小黑板和4块B型小黑板共需820元.
(1)求购买一块A型小黑板、一块B型小黑板各需多少元.
(2)根据该中学实际情况,需从公司购买A,B两种型号的小黑板共60块,要求购买A,B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量不小于购买B型小黑板数量的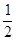 .则该中学从公司购买A,B两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
.则该中学从公司购买A,B两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
计算:5+(-6)+3+9+(-4)+(-7);
计算: (-8)+10+2+(-1);
计算:
(1)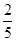 +(-
+(-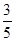 ); (2)(-
); (2)(-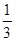 )+(-
)+(-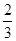 ); (3)(-
); (3)(-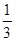 )+
)+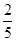 ; (4)(-
; (4)(- )+(-
)+(- );
);
(5)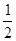 +(-2
+(-2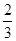 ); (6)(-
); (6)(-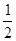 )+(-1
)+(-1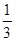 ); (7)(-1
); (7)(-1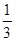 )+(-2
)+(-2 ); (8)3
); (8)3 +(-1
+(-1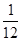 );
);
计算:
(1)(-0.9)+(-2.7); (2)3.8+(-8.4); (3)(-0.5)+3; (4)3.92+1.78;
(5)7+(-3.04); (6)(-2.9)+(-0.31); (7)(-9.18)+6.18; (8)4.23+(-6.77);
计算:
(1)(-10)+(+6); (2)(+12)+(-4); (3)(-5)+(-7); (4)(+6)+(+9);
(5)67+(-73); (6)(-84)+(-59); (7)33+48; (8)(-56)+37;