如图甲,单匝圆形线圈c与电路连接,电阻R2两端与平行光滑金属直导轨p1e1f1、p2e2f2连接.垂直于导轨平面向下、向上有矩形匀强磁场区域Ⅰ、Ⅱ,它们的边界为e1e2,区域Ⅰ中垂直导轨并紧靠e1e2平放一导体棒ab.两直导轨分别与同一竖直平面内的圆形光滑绝缘导轨o1、o2相切连接,o1、o2在切点f1、f2处开有小口可让ab进入,ab进入后小口立即闭合.已知:o1、o2的直径和直导轨间距均为d,c的直径为2d;电阻R1、R2的阻值均为R,其余电阻不计;直导轨足够长且其平面与水平面夹角为 ,区域Ⅰ的磁感强度为B0.重力加速度为g.在c中边长为d的正方形区域内存在垂直线圈平面向外的匀强磁场,磁感强度B随时间t变化如图乙所示,ab在t=0~
,区域Ⅰ的磁感强度为B0.重力加速度为g.在c中边长为d的正方形区域内存在垂直线圈平面向外的匀强磁场,磁感强度B随时间t变化如图乙所示,ab在t=0~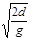 内保持静止.
内保持静止.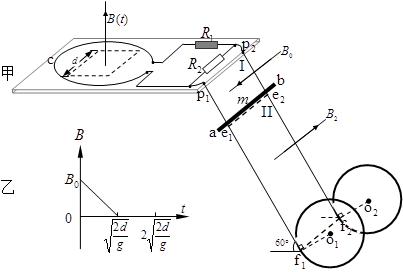
(1)求ab静止时通过它的电流大小和方向;
(2)求ab的质量m;
(3)设ab进入圆轨道后能达到离f1f2的最大高度为h,要使ab不脱离圆形轨道运动,求区域Ⅱ的磁感强度B2的取值范围并讨论h与B2的关系式.
已知月球绕地球运动周期T和轨道半径r,地球半径为R求(1)地球的质量?(2)地球的平均密度?
如图所示,离质量为M、半径为R、密度均匀的球体表面R远处有一质量为m的质点,此时M对m的万有引力为F1 ;当从M中挖去一半径为r= R的球体时,剩下部分对m的万有引力为F2.则F1与F2之比是多少?
R的球体时,剩下部分对m的万有引力为F2.则F1与F2之比是多少?
如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速率弹回,又与m1碰撞,再一次碰撞后两球都静止.求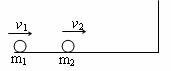
(1)第一次碰后m1球速度的大小
(2)两次碰撞中两球损失的总机械能
一个质量为0.2kg、以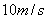 的速度飞来的网球被球拍击中,并以
的速度飞来的网球被球拍击中,并以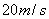 的速度反方向弹回,网球与球拍的接触时间为
的速度反方向弹回,网球与球拍的接触时间为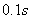 ,试求:(不考虑重力的冲量)
,试求:(不考虑重力的冲量)
(1)网球动量的变化
(2)球拍对网球的平均作用力
今有一质量为M的气缸,用质量为m的活塞封有一定质量的理想气体,当气缸水平横放时,空气柱长为L0(如图甲所示),若将气缸按如图乙悬挂保持静止时,求气柱长度为多少?已知大气压强为P0,活塞的横截面积为S,它与气缸之间无摩擦且不漏气,且气体温度保持不变.