如图所示,一带电荷量为+q、质量为m的小物块处于一倾角为37°的光滑斜面上,当整个装置置于一水平向右的匀强电场中,小物块恰好静止.重力加速度为g,(sin37°=0.6,cos37°=0.8)求: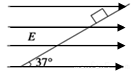
(1)水平向右的电场的电场强度;
(2)若将电场强度减小为原来的一半,小物块的加速度是多大。
一个小铁球从高空某处以初速度v0 =2m/s竖直向下抛,做加速度大小a =10m/s2,方向竖直向下的匀加速直线运动,求:
(1)小铁球从开始运动到第3s初的速度;
(2)小铁球运动过程中第4s内的位移.(说明:在此运动时间内小球均未落地)
甲乙两车在同一轨道上同向行驶,甲车在前以20m/s的速度匀速行驶,乙车在后以10m/s的速度匀速行驶。当两车相距24m时,甲车开始刹车,加速度大小为2m/s2。问经多少时间乙车可追上甲车?
2010年4月15日,奥地利施第里尔州高空2000m处进行了极其危险的特技表演项目,场面震撼和令人揪心。如右图所示,若跳伞运动员做低空跳伞表演,他在离地面224m高处,由静止开始在竖直方向做自由落体运动。一段时间后,立即打开降落伞,以12.5m/s2的平均加速度匀减速下降,为了运动员的安全,要求运动员落地速度最大不得超过5m/s。求运动员展开伞时,离地面高度至少为多少?着地时相当于从多高处自由落下?(g取10m/s2)
(附加题)一吊桥由六对钢杆悬吊着,六对钢杆在桥面分列两排,其上悬挂在两根钢缆上,如图为其一截面图。已知图中相邻两钢杆间距离为9m,靠桥面中心的钢杆长度为2m(即 ),),BB′=EE',CC′=PP',又已知两端钢缆与水平成45°角,若自重不计,为使每承受负荷相同,试求钢杆BB′和CC′的长度应各为多少?
),),BB′=EE',CC′=PP',又已知两端钢缆与水平成45°角,若自重不计,为使每承受负荷相同,试求钢杆BB′和CC′的长度应各为多少?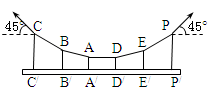
如图所示,光滑固定斜面上有一个质量为10kg的小球被轻绳拴住悬挂在天花板上,已知绳子与竖直方向的夹角为450,斜面倾角为300,整个装置处于静止状态。(g=10m/s2)求:(所有结果均保留三位有效数字)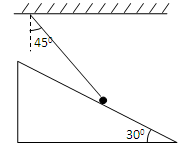
(1)绳中拉力的大小和斜面对小球支持力的大小;
(2)若在竖直面内另外用一个外力拉小球,能够把小球拉离斜面,求最小的拉力的大小。