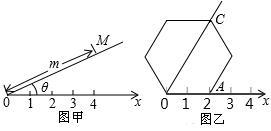
（2014年湖南常德3分）阅读理解：如图甲，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．
应用：在图乙的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（ ）
| A．（60°，4） | B．（45°，4） |
C． |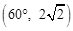
D． |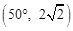
如图，已知AB=AC，AE=AF，BE与CF交于点D，则①△ABE≌△ACF；②△BDF≌△CDE；③D在∠BAC的平分线上，以上结论中，正确的是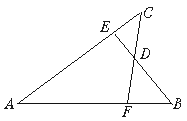
| A．只有① | B．只有② |
| C．只有①和② | D．①②与③ |
如左下图，在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于D，如果AC=3cm，那么AE+DE等于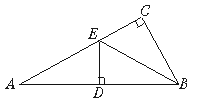
| A．2cm | B．3cm | C．4cm | D．5cm |
下列命题中是真命题的是
| A．有两角及其中一角的平分线对应相等的两个三角形全等 |
| B．相等的角是对顶角 |
| C．余角相等的角互余 |
| D．两直线被第三条直线所截，截得的同位角相等 |
下列各语句中，不是真命题的是
| A．直角都相等 | B．等角的补角相等 |
| C．点P在角的平分线上 | D．对顶角相等 |
已知二次函数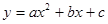
（
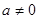）的图象如图所示，有下列结论：⑴abc>0；⑵a+b+c>0；⑶a-b+c<0；其中正确的结论有（）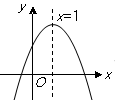
| A．0个 | B．1个 | C．2个 | D．3个 |