（2014年湖北天门学业10分）某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作．已知该水果的进价为8元/千克，下面是他们在活动结束后的对话．
小丽：如果以10元/千克的价格销售，那么每天可售出300千克．
小强：如果每千克的利润为3元，那么每天可售出250千克．
小红：如果以13元/千克的价格销售，那么每天可获取利润750元．
【利润=（销售价-进价）
销售量】
（1）请根据他们的对话填写下表：
| 销售单价x（元/kg） |
10 |
11 |
13 |
| 销售量y（kg） |
|
|
|
（2）请你根据表格中的信息判断每天的销售量y（千克）与销售单价x（元）之间存在怎样的函数关系．并求y（千克）与x（元）（x＞0）的函数关系式；
（3）设该超市销售这种水果每天获取的利润为W元，求W与x的函数关系式．当销售单价为何值时，每天可获得的利润最大？最大利润是多少元？
对非负实数x“四舍五入”到个位的值记为
即：当n为非负整数时，如果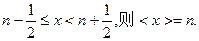
如：<0>=<0.48>=0，<0.64>=<1.493>=1，<2>=2，<3.5>=<4.12>=4，…
试解决下列问题：
（1）填空：①
=（
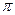为圆周率）；
②如果
的取值范围为；
（2）①当
；
②举例说明
不恒成立；
（3）求满足
的值；
（4）设n为常数，且为正整数，函数
范围内取值时，函数值y为整数的个数记为
的个数记为b.
求证：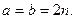
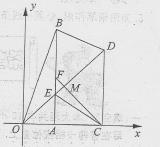
如图，在直角坐标系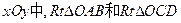
的直角顶点A，C始终在x轴的正半轴上，B，D在第一象限内，点B在直线OD上方，OC=CD，OD=2，M为OD的中点，AB与OD相交于E，当点B位置变化时，
试解决下列问题：
（1）填空：点D坐标为；
（2）设点B横坐标为t，请把BD长表示成关于t的函数关系式，并化简；
（3）等式BO=BD能否成立？为什么？
（4）设CM与AB相交于F，当△BDE为直角三角形时，判断四边形BDCF的形状，并证明你的结论.
如图，已知△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，过D作DE⊥BC，垂足为E，连结OE，CD=
，∠ACB=30°.
（1）求证：DE是⊙O的切线；
（2）分别求AB，OE的长；
（3）填空：如果以点E为圆心，r为半径的圆上总存在不同的两点到点O的距离为1，则r的取值范围为.
海宝在研究数学问题时发现了一个有趣的现象：
（1）请你用数学表达式补充完整海宝发现的这个有趣的现象；
（2）请你证明海宝发现的这个有趣现象.
实践应用（本小题满分6分）
有200名待业人员参加某企业甲、乙、丙三个部门的招聘，到各部门报名的人数百分比见图表1，该企业各部门的录取率见图表2.（部门录取率=
×100%）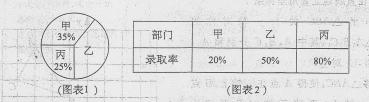
（1）到乙部门报名的人数有人，乙部门的录取人数是人，该企业的录取率为；
（2）如果到甲部门报名的人员中有一些人员改到丙部门报名，在保持各部门录取率不变的情况下，该企业的录取率将恰好增加15%，问有多少人从甲部门改到丙部门报名？