(2014年福建漳州14分)已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.

已知:如图, 中,
中, ,
,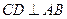 于
于 ,
, 平分
平分 ,且
,且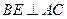 于
于 ,与
,与 相交于点
相交于点 是
是 边的中点,连结
边的中点,连结 与
与 相交于点
相交于点 .
.
(1)求证: ≌
≌ ;
;
(2)求证: 。
。
某工厂有 甲、乙两个蓄水池,将甲池中的水以每小时5立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,结合图象回答下列问题:
甲、乙两个蓄水池,将甲池中的水以每小时5立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,结合图象回答下列问题:
(1)分别求出甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数关系式(不写自变量x的取值范围);
(2)算出注水多长时间后甲、乙两个蓄水池水的深度相同?
(3)当两个蓄水池水深相同时,水深是多少?并求出甲蓄水池刚开始里面的蓄水量是多少立方米?
为了美化环境,在一块正方形空地上分别种植四种不同的花草。现将这块空地按下列要求分成四块:⑴分割后的整个图形必须是轴对称图形;⑵四块图形形状相同;⑶四块图形面积相等。现已有两种不同的分法:
(1)分别作两条对角线(图11)
(2)过一条边的三等分点作这边的垂线段(图12)
(图12中两个图形的分割看作同一 方法)
方法)
请你按照上述三个要求,分别在下面三个 正方形中给出另外三种不同的分割方法(只要求正确画图,不写画法).
正方形中给出另外三种不同的分割方法(只要求正确画图,不写画法).
在平面直角坐标系中,已知直线经过A(-3,7)、B(2,-3)两点。
(1)求经过A、B两点的一次函数关系式;
(2)画出该一次函数的图象。
(1)
(2)