如图所示，在x轴上方有垂直xoy平面向里的匀强磁场，磁感应强度为B1=B0，在x轴下方有交替分布的匀强电场和匀强磁场，匀强电场平行于y轴，匀强磁场B2=2B0垂直于xoy平面，图象如图所示。一质量为m，电量为-q的粒子在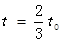
时刻沿着与y轴正方向成60°角方向从A点射入磁场，
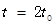时第一次到达x轴，并且速度垂直于x轴经过C点，C与原点O的距离为3L。第二次到达x轴时经过x轴上的D点，D与原点O的距离为4L。(不计粒子重力，电场和磁场互不影响，结果用B0、m、q、L表示。)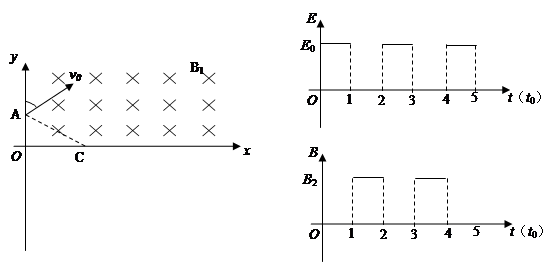 
（1）求此粒子从A点射出时的速度υ0。
（2）求电场强度E0的大小和方向。
（3）粒子在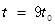
时到达M点，求M点坐标。
中国航天局将如图所示的标志确定为中国月球探测工程形象标志。它以中国书法的笔触，抽象地勾勒出一轮明月，一双脚印踏在其上，象征着月球探测的终极梦想。2007年10月24日18：05时“嫦娥1号”探月卫星成功发射，最后绕月球做匀速圆周运动。已知“嫦娥1号”距离月球表面高度为h，月球表面重力加速度为g，月球半径为R，求：
（1）“嫦娥1号”绕月飞行的周期T=？
（2）在月球表面上发射一颗绕它运行的卫星的的最小发射速度为多少？
如图所示，半径为R，内壁光滑的半圆形轨道竖直放置，质量为m的小球以某一速度进入圆形轨道，通过最高点C时，对轨道的压力为3mg，AC在同一竖线上，不计空气阻力，求：
（1）小球从A到B的过程中克服重力所做的功；
（2）小球落至水平面上时距离A点的水平距离。
一质量为m＝40kg的小孩子站在电梯内的体重计上。电梯从t＝0时刻由静止开始上升，在0到6s内体重计示数F的变化如图所示。试问：在这段时间内电梯上升的高度是多少？取重力加速度g＝10m/s2。
一个质量为
的物体静止在足够大的水平地面上，物体与地面间的动摩擦因数
。从
开始，物体受到一个大小和方向呈周期性变化的水平力F作用，力F随时间的变化规律如图10所示。求83秒内物体的位移大小和力F对物体所做的功。
取
。
注意：这种题应考虑是周期性问题
一水平的浅色长传送带上放置一煤块（可视为质点），煤块与传送带之间的动摩擦因数为μ。初始时，传送带与煤块都是静止的。现让传送带以恒定的加速度a0开始运动，当其速度达到v0后，便以此速度做匀速运动。经过一段时间，煤块在传送带上留下了一段黑色痕迹后，煤块相对于传送带不再滑动。求此黑色痕迹的长度。