（年广东深圳9分）如图，直线AB的解析式为y=2x+4，交x轴于点A，交y轴于点B，以A为顶点的抛物线交直线AB于点D，交y轴负半轴于点C（0，﹣4）．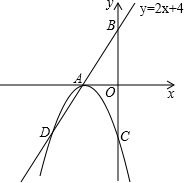
（1）求抛物线的解析式；
（2）将抛物线顶点沿着直线AB平移，此时顶点记为E，与y轴的交点记为F，
①求当△BEF与△BAO相似时，E点坐标；
②记平移后抛物线与AB另一个交点为G，则S△EFG与S△ACD是否存在8倍的关系？若有请直接写出F点的坐标．
（本小题满分8分）（1）如图1,大圆面积为5,请应用旋转知识,画图说明空白部分的面积.
(2)如图2,大正方形边长为9个单位长,阴影部分的宽为1个单位长,请应用平移知识,画图说明空白部分的面积.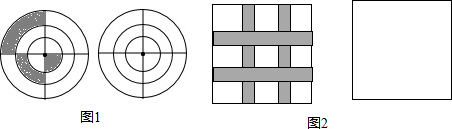
如图，△ABC中，AD为∠BAC的平分线，AD的垂直平分线EF交BC的延长线于点F，连接AF．求证：∠B=∠CAF．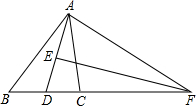
（本小题满分8分）为使代数式x2一ax一20在整数范围内可以因式分解，其中的整数a可以有多少?刘学峰说有6个，宋世杰说有5个，杨萌说有无穷个．你认为他们谁说得对?为什么?
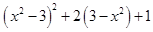分解因式．
(1)关于x的方程2x一3=2m+8的解是负数，求m的取值范围．
(2)如果代数式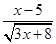
有意义，求x的取值范围．