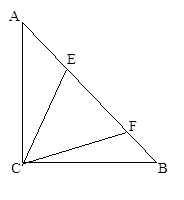
(年江苏南通13分)如图,矩形ABCD中,AB=3,AD=4,E为AB上一点,AE=1,M为射线AD上一动点,AM=a(a为大于0的常数),直线EM与直线CD交于点F,过点M作MG⊥EM,交直线BC于G.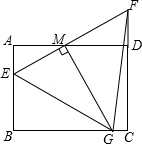
(1)若M为边AD中点,求证:△EFG是等腰三角形;
(2)若点G与点C重合,求线段MG的长;
(3)请用含a的代数式表示△EFG的面积S,并指出S的最小整数值.
(本小题满分6分)尺规作图:已知线段a,作一个等腰 ,使底边长为a,底边上的高为
,使底边长为a,底边上的高为 .(要求:写出已知求作,保留作图痕迹,在所作图中标出必要的字母,不写作法和结论)
.(要求:写出已知求作,保留作图痕迹,在所作图中标出必要的字母,不写作法和结论)
已知:
求作:
(本小题满分6分)解不等式组 .
.
运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法. 如图1,在等腰三角形ABC中,AB=AC,AC边上的高为
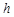 ,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为
,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为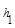 、
、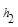 .连接AM,可得结论
.连接AM,可得结论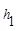 +
+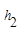 =
=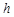 .当点M在BC延长线上时,
.当点M在BC延长线上时,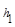 、
、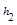 、
、 之间的等量关系式是.(直接写出结论不必证明).
之间的等量关系式是.(直接写出结论不必证明).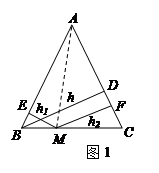
应用:平面直角坐标系中有两条直线
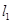 :
: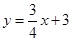 、
、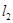 :
: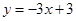 ,若
,若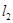 上的一点M到
上的一点M到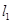 的距离是1.请运用(1)的条件和结论求出点M的坐标.
的距离是1.请运用(1)的条件和结论求出点M的坐标.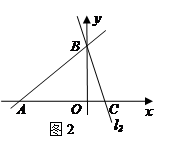
张老师于2010年9月份在杭州买了一套楼房,当时(即9月份)在建行贷款96万元,贷款期限为20年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%(每月还款数额=平均每月应还的贷款本金+月利息,月利息=上月所剩贷款本金数额×月利率).求张老师借款后第一个月的还款数额.
假设贷款月利率不变,请写出张老师借款后第n(n是正整数)个月还款数额p与n之间的函数关系式(不必化简).
在(2)的条件下,求张老师2011年10份的还款数额.
已知△ABC,∠ACB=90º,AC=BC,点E、F在AB上,∠ECF=45º,设△ABC的面积为S,说明AF·BE=2S的理由。